Gudrun sprach im Januar 2024 mit zwei Studenten ihrer Vorlesung Mathematical Modelling and Simulation: Lukas Ullmer und Moritz Vogel. Sie hatten in ihrem Projekt Wahlmodelle ananlysiert. In dem Gespräch geht es darum, wie man hierfür mathematische Modelle findet, ob man Wahlsysteme https://de.wikipedia.org/wiki/Wahlsystem fair gestalten kann und was sie aus den von ihnen gewählten Beispielen gelernt haben. Der Fokus ihrer Projektarbeit liegt auf der Betrachtung und Analyse von Wahlen, in denen mehrere verschiedene Wähler zu einem Thema abstimmen. Formal von Relevanz sind hierbei die sogenannten Wahlsysteme https://de.wikipedia.org/wiki/Wahlsystem, welche die Art der Aggregation der Wählerstimmen beschreiben. Diese fallen in der Praxis recht vielfältig aus und über die Jahre wurden verschiedenste Wahlsysteme vorgeschlagen, angewendet und auch analysiert. In dieser Arbeit werden drei Kategorien präferenzbasierter Wahlsysteme analysiert: vergleichsbasierte Systeme, Scoring-Systeme sowie Approval-Systeme. Aufbauend darauf erfolgt die Konstruktion mehrstufiger und hybrider Wahlsysteme. Desweiteren werden verschiedenen Wahleigenschaften wie z.B. die Nicht-Diktatur oder die Strategiesicherheit betrachtet. Diese meist wünschenswerten Eigenschaften schließen sich teilweise gegenseitig aus. Die Themen Wahlmanipulation und Wahlkontrolle liegen deshalb besonders im Fokus. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

16m

Feb 10, 2024

In dieser Folge geht es darum, wie Sebastian und Gudrun Mathematik an Hochschulen unterrichten und welche Rollen das Medium Podcast und konkret unser Podcast Modellansatz dabei spielen. Die Fragen stellte unsere Hörerin Franziska Blendin, die in der Folge 233 http://modellansatz.de/fernstudium-maschinenbau im Jahr 2020 über Ihr Fernstudium Bachelor Maschinenbau http://modellansatz.de/fernstudium-maschinenbau berichtet hatte. Sie hatte uns vorab gefragt: "Was versprecht ihr euch von dem Podcast - was ist euer Fazit nach den Jahren den ihr ihn schon macht und wie gestaltet ihr warum Lehre? Was macht euch Spaß, was sind Herausforderungen, was frustriert euch? Warum und wie gestaltet ihr Lehre für Studierende außerhalb der Mathematik, also beispielsweise Maschinenbau?" Es ist ein bisschen lustig, dass die erste Folge Modellansatz, in der Sebastian und Gudrun sich spontan ein Thema zum reden suchten ausgerechnet ein Gespräch über eine neu konzipierte Vorlesung war und der Podcast diese Vorlesung bis heute in unterschiedlichen Rollen begleitet, obwohl das nicht zum ursprünglichen Plan gehörte, wie wir uns einen Podcast über Mathematik vorgestellt hatten. Einerseits haben viele kein Verständnis dafür, was alles mit Mathe gemacht werden kann, andererseits erleben wir intern andauernd so viele spannenden Vorträge und Personen. Eigentlich bringen wir die beiden Sachen in unserem Podcast nur zusammen. Das Medium Podcast ist dabei durch das Gespräch sehr niederschwellig: Es ist so sehr leicht mit den Gesprächen in die Themen einzusteigen und auch auf viel weiteren Ebenen sich darüber zu unterhalten. Wir sind überzeugt, dass wir mit Text oder Video nie so viele und so umfangreiche Austauschsformen einfangen können, mal ganz abgesehen davon, dass die Formate dann an sich für uns zu einer viel größeren Herausforderung in Form und Darstellung geworden wären. Wir hoffen, dass sich irgendwann auch mal eine Person dazu bekennt, wegen unseres Podcasts ein Mathe- oder Informatikstudium zu erwägen, aber bisher ist das tolle Feedback an sich ja schon eine ganz ausgezeichnete Bestätigung, dass diese Gespräche und Themen nicht nur uns interessieren. Viele der Gespräche haben sich auch schon vielfach für uns gelohnt: Sebastian hat aus vielen Gesprächen Inspirationen für Vorlesungen oder andere Umsetzungen gewonnen. Ein Fazit ist auf jeden Fall, dass das Ganze noch lange nicht auserzählt ist, aber wir auch nicht außerhalb unserer Umgebung leben. In der Pandemie sind einerseits Gespräche am Tisch gegenüber, wie wir sie gerne führen, schwierig geworden, und gleichzeitig ist die Lehre so viel aufwendiger geworden, dass kaum Zeit verblieb. Aufnahmen, waren zuletzt hauptsächlich "interne" Podcasts für Vorlesungen, damit die Studierenden daheim und unterwegs sich mit den Inhalten auseinandersetzen können. Gudrun hat damit auch Themen vorbereitet, die sie anschließend in die Zeitschrift Mitteilungen der Deutschen Mathematiker-Vereinigung als Artikel geschrieben hat. Das betrifft insbesondere die Folgen zu Allyship und zum Mentoring in der Mathematik. In der Vermittlung von Mathematik im Studium gibt es kaum Themen, die nicht irgendwo spannend und interessant sind. Um die Themen zu verstehen oder wie dort die Lösungen oder Verfahren gefunden wurden, muss die Theorie behandelt und in weiten Teilen verstanden werden. Da aber "Rosinenpickerei" nichts bringt (also nur die nötigsten Teile von Theorie zu erzählen), geht es darum, ein sinnvolles Mittelmaß zu finden. Also auf der einen Seite ein gutes Fundament aufzubauen zu einem Thema, aber gleichzeitig noch Zeit für Einblicke in spannende und interessante Teile zu haben. Es ist in der Vorbereitung auf der einen Seite total schön, wenn dann eine Anwendung perfekt in die Theorie passt, beispielsweise entwirft Sebastian gerade ein Skript zu formalen Sprachen und Grammatiken, und dann kann man das Komprimierverfahren LZW https://de.wikipedia.org/wiki/Lempel-Ziv-Welch-Algorithmus als eine dynamische Grammatik sehen. Oder es geht um theoretische und "langweilige" Zustandsmaschinen und dann gibt es das Beispiel, dass die Raspberry Pi Foundation gerade dazu einen eigenen Chip (RP2040 https://www.raspberrypi.com/documentation/microcontrollers/rp2040.html) mit solchen Komponenten veröffentlicht, oder mit dem Newton-Verfahren wurde die schnelle Quadratwurzel für das Computerspiel Quake https://media.ccc.de/v/gpn20-91-0x5f3759df-ein-wtf-fr-mehr-fps erst möglich. Ob das dann auch so toll in der Vorlesung herüberkommt, ist nochmal ein eigenes Thema, aber wenn es klappt, so ist das natürlich großartig. Umgekehrt frustriert es dann schon, wenn die Grundlagen nicht bei möglichst vielen ankommen- nicht jede Person muss sich ja bis ins letzte für ein Thema begeistern, aber am Ende sollte der Großteil die wichtigen Hauptsachen mitnehmen. Leider gibt es immer ein paar Leute, wo das dann trotz vieler Angebote leider nicht so gut klappt, und das frustriert natürlich. Dann muss geschaut werden, woran es liegen könnte. Aktuell hilft das Nörgeln und Nerven, wenn nicht regelmäßig die angebotenen Übungsaufgaben abgegeben werden, wohl mit am Besten. Warum werden mathematische Themen im Ingenieurstudium relevant: Das hängt ganz davon ab, welche Kurse wir haben, und was gebraucht wird... Sebastian unterrichtet jetzt gerade Informatik-Studierende und in den Wirtschaftswissenschaften, früher außer MACH/CIW/BIW/MAGE... auch mal Mathe-Lehrende. Das "Wie" ist dann jeweils auf die Gruppe zugeschnitten: Zunächst gibt es ja unterschiedliche Voraussetzungen: Curriculum, Haupt- & Nebenfächer, etc.. Dann gibt es eine Liste von Fertigkeiten, die vermittelt werden sollen und können, und dann besonders in den Vorlesungen außerhalb des Mathematik-Studiums die lästige Beschränkung des Umfangs der Veranstaltung, und wieviel Eigenarbeit erwartet werden kann. Grundsätzlich möchten wir auch bei den Nicht-Hauptfächlern so viel davon erzählen, was dahinter steht- statt "ist halt so"- und was heute damit gemacht werden kann. Diese Motivation macht vielen das Lernen leichter. Es muss aber auch immer viel selbst gemacht werden, dh. viele Aufgaben und prototypische Problemlösungen, denn Mathe lernt sich nicht durchs zuhören alleine. (leider... ;) Damit geht das Puzzle-Spiel los: Welche Grundlagen müssen aufgebaut werden, und was kann wie in der gegebenen Zeit sinnvoll behandelt werden... Und natürlich immer mit dem Blick darauf, ob es Anküpfungspunkte in die Studienrichtungen der Studierenden gibt. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS VON FRANZISKA __ __ PODCASTS ZUM THEMA MATHE IN DER HOCHSCHULLEHRE __ __ PODCASTS ALS PROJEKTABSCHLUSS __ __ WEITERE ERWÄHNTE PODCASTS, ARTIKEL UND VORTRÄGE __ __

1h 42m

Oct 03, 2023

Gudrun unterhält sich in dieser Folge mit Waltraud Kahle. Sie war bis 2018 als außerplanmäßige Professorin in der Fakultät für Mathematik https://www.math.ovgu.de/ an der Otto von Guericke Universität https://www.ovgu.de/ in Magdeburg beschäftigt und war Mitglied des Instituts für Mathematische Stochastik https://www.math.ovgu.de/Institute/IMST.html. Das Thema des Gespräches ist das Forschungsthema von Waltraud: Statistik für zensierte Daten und in Abnutzungsprozessen sowie unvollständige Reparatur. Das Gespräch beginnt mit der Frage: Wie kann man Aussagen darüber treffen, wie lange technische Objekte oder auch Menschen "leben" . Ungefähre Aussagen hierzu für große Gruppen sind in der Industrie, der Demographie und Versicherungsmathematik und Medizin nötig. Es ist ein statistisches Problem, das sich in der Theorie auf eine (möglichst große) Anzahl von Beobachtungen bezieht aus denen dann Schlussfolgerungen abgeleitet werden, die für ähnliche Prozesse auch zu Vorhersagen dienen können. In der Praxis liegen aber in der Regel nur zensierte Daten https://de.wikipedia.org/wiki/Zensierte_Daten vor, denn die Beobachtung muss abgebrochen werden, bevor die vollständige Information vorliegt. Ein alternativer Zugang ist es nun, nicht nach der Lebensdauer zu fragen sondern die der Lebensdauer zugrunde liegenden Abnutzungsprozesse zu modellieren (z.B. Verschleiß und Ermüdung). Hier verwendet man stochastische Prozesse, wie zum Beispiel den Wienerprozess https://de.wikipedia.org/wiki/Wienerprozess. Grundlegende Eigenschaft des Wienerprozesses ist es, dass in jedem Zeitintervall ein normalverteilter Zuwachs erfolgt und alle diese Zuwächse voneinander unabhängig sind. Ein Ausfall erfolgt, wenn der Abnutzungsprozess ein vorgegebenes Niveau erstmalig erreicht. Man fragt sich folglich: Wie ist die Verteilung dieser "Erstüberschreitungszeit". Zur Vermeidung von Ausfällen können regelmäßig vorbeugende Instandhaltungsmaßnahmen durchgeführt werden, die das Abnutzungsniveau verringern. Das kann mit festen Intervallen oder nach vorgegebenen Ereignissen stattfinden. Zu DDR-Zeiten gab es z.B. ein Projekt, dass sicherstellen konnte, das notwendige Wartungsarbeiten von Mähdreschern nur im Winter erfolgten, damit sie zur Erntesaison voll einsatzfähig waren. Das statistische Modell muss Aussagen zu folgenden Fragen treffen können __ __ Andere Modellierungsmöglichkeiten bieten Gammaprozesse oder inhomogene Poissonprozesse https://de.wikipedia.org/wiki/Poisson-Prozess. Im Gespräch gehen Gudrun und Waltraud auf Eigenschaften der Normalverteilung https://de.wikipedia.org/wiki/Normalverteilung ein. Sie besprechen die Exponentialverteilung https://de.wikipedia.org/wiki/Exponentialverteilung (diese hat eine konstante Ausfallrate https://de.wikipedia.org/wiki/Ausfallrate). Das beschreibt elektronische Bauteile mit langer Lebensdauer sehr gut. Außerdem geht es um die Weibull-Verteilung https://de.wikipedia.org/wiki/Weibull-Verteilung. Diese passt auf Systeme mit sehr vielen Teilen (das Modell nimmt hier sogar unendlich viele Teile), die mit geringer Wahrscheinlichkeit ausfallen und wo das System ausfällt, sobald das erste Glied ausgefallen ist. Diese Verteilung hat die praktische Eigenschaft, dass die in der Medizin verwendeten Modelle der proportionalen Ausfallrate und der proportionalen Lebensdauer übereinstimmen. Waltraud engaiert sich im eLeMeNTe https://www.elemente.org/ e.V.. Das ist der Landesverein Sachsen-Anhalt zur Förderung mathematisch, naturwissenschaftlich und technisch interessierter und talentierter Schülerinnen, Schüler und Studierender. Ein Ziel ist es, die Landesolympiaden Mathematik in Sachsen-Anhalt durchzuführen und Schülerinnen und Schüler mit speziellen Arbeitsgemeinschaften auf die Wettbewerbe vorzubereiten. Waltraud findet es spannend, dort oft überraschenden Ideen der Kinder und jungen Leute zu begegnen, die noch nicht in den ausgetretenen Denkpfaden unterwegs sind. Zur Geschichte der Mathe-Olympiaden https://de.wikipedia.org/wiki/Mathematik-Olympiade_in_Deutschland finden sich auf Wikipedia folgende Informationen (die Gudrun aus eigenem Erleben bestätigen kann): "Die erste Mathematik-Olympiade in der DDR fand 1961/62 als „Olympiade Junger Mathematiker“ statt. Seitdem gab es dort ab der 5. Klassenstufe Schul- und Kreisolympiaden, ab der 7. Klassenstufe Bezirksolympiaden und ab der 10. Klassenstufe DDR-Olympiaden, an der aber auch sogenannte Frühstarter aus tieferen Klassenstufen teilnahmen. Der DDR-Ausscheid fand zunächst in der Woche vor Ostern jeden Jahres in der Jugendhochschule „Wilhelm Pieck“ bei Berlin, später im Mai in Erfurt statt. ... Auf allen Ebenen gab es zur Unterstützung begabter Schüler Mathematikzirkel....Nach der Wiedervereinigung Deutschlands entwickelte sich die Mathematikolympiade schnell zu einem bundesweiten Schülerwettbewerb. Seit 1994 ist der Mathematik-Olympiaden e.V. Träger des Wettbewerbs, der in Kooperation mit dem Talentförderzentrum Bildung & Begabung jährlich ausgeschrieben wird. Seit 1996 nehmen alle 16 Bundesländer an der Bundesrunde teil." Die Bundesrunde fand 1993, 1994 und 2001 in Magdeburg stattt. * REFERENZEN UND WEITERE INFORMATIONEN __ __ __ __

49m

Nov 06, 2022

Gudrun spricht in dieser Folge mit Anshuman Chauhan https://www.mvm.kit.edu/Mitarbeiter_MVM_5811.php über sein Masterstudium Computational Sciences in Engineering https://www.tu-braunschweig.de/cse/what-is-cse (CSE) an der TU Braunschweig https://www.tu-braunschweig.de/. CSE ist dort ein viersemestriger Masterstudiengang, der etwa zur Hälfte in Englisch und zur anderen Hälfte in Deutsch unterrichtet wird. Er ist an der Fakultät Architektur, Bauingenieurwesen und Umweltwissenschaften angesiedelt, kombiniert aber in der Ausbildung Ingenieurwissenschaften, Mathematik und angewandte Informatik. In gewisser Weise ist es eine konsequente Weiterentwicklung der Idee der Technischen Universitäten deutscher Prägung, dass heute solche interdisziplinären Studiengänge angeboten werden. So wie das heutige KIT wurden sie ja häufig als Polytechnische Schulen gegründet, in denen zunächst das was wir heute Maschinenbau nennen mathematisiert wurde, um mit der Entwicklung der Technik Schritt halten zu können. In zunehmenden Maße waren dann immer mehr technische Fächer ohne eigene Forschung und auch ohne eine Grundausbildung in Mathematik nicht mehr denkbar. Heute hält nun endgülitg zunächst die Computersimulation aber zunehmend auch die Benutzung von Algorithmischem Lernen und Big Data Einzug in die Ingenieurwissenschaften. Diese Entwicklung wird mit Spezialisierungen in der Mathematik, insbesondere in den Studiengängen Technomathematik, in Spezialisierungen in den Ingenieurwissenschaften, aber auch durch die Schaffung von neuartigen Studiengängen begleitet, die im Namen wie in der Ausbildung mindestens zwei, oft aber drei Standbeine haben: Mathematik, Informatik und eine technische Anwendung. Anshuman ist in Neu-Dehli aufgewachsen. Nach seiner Bachelorarbeit zu Finite Element Methoden hatte er sich weltweit nach Studiengängen umgeschaut, die mit Computersimulation zu tun haben - am liebsten mit Aerodynamik für Autos. Deutschland war für ihn dabei attraktiv, weil es renommierte Technische Universitäten hat und die Kosten nicht exorbitant sind. Er entschied sich für die TU in Braunschweig aufgrund eben dieses Renomees der deutschen TU9 https://de.wikipedia.org/wiki/TU9. Sie hat zur Zeit etwa 20.000 Studierende in fast 80 Studiengänge. Seit 2018 gibt es einen Exzellenzcluster in Luftfahrt und Metrologie und der DLR ist in der Nähe. Im Gespräch erläutert Anshuman, dass er mit der Entscheidung für Braunschweig und für diesen Studiengang sehr zufrieden ist. Er ist nun nach erfolgreichem Abschluss und einiger Zeit in der Wirtschaft seit 2020 am KIT im Graduiertenkolleg SiMet https://www.simet.kit.edu/, wo der Kontakt mit dem Podcast zustande kam. Braunschweig hat ein richtiges Stadtleben, das von den vielen Studierenden dort mit geprägt ist. Anshuman ist dort in einem Studentenwohnheim untergekommen und hatte sofort sozial Anschluss. In dem von ihm in Braunschweig belegten Masterprogramm CSE ist jedes Semester aufgeteilt zwischen Ingenieurfächern, Mathematik und Informatik. Zum Beispiel die Fächer Strömungsdynamik und Thermodynamik zusammen mit partiellen Differentialgleichungen in der Mathematik und Visualisierung im Informatikteil. Später sind dann Vertiefungskurse in z.B. Maschinenbau, Elektrotechnik, Bauingenieurwesen oder Informatik wählbar. Die Numerischen Methoden in der Aerodynamik z.B. waren sehr praxisnah. Er wollte seine Masterarbeit unbedingt in der Industrie schreiben, um Erfahrung in einem Unternehmen zu sammeln. Er sah aber sehr schnell, dass richtig Deutsch zu lernen dafür eine notwendige Voraussetzung ist. Deshalb nahm er sich ein Semester Zeit, um die Sprache noch besser zu üben und außerdem einige für ihn sehr interessante Kurse zu belegen, zu denen er vorher keine Zeit gehabt hatte. Überdies hat er auch noch spanisch belegt. Mit der deutschen Bewerbung hat es schließlich mit einer Masterarbeit in Stuttgart geklappt. Der Wechsel von Braunschweig in Norddeutschland nach Stuttgart in Süddeutschland war für ihn sehr spürbar - es ist einfach ein anderer Schlag Menschen. In der Firma gibt es natürlich vorgeschriebene Prozesse, in die man sich erst einarbeiten muss. Sie bringen aber eine gewisse Robustheit in die Entwicklung. Als Masterstudent hatte er trotzdem genug Freiheit und eine tolle Betreuung. In der Industrietätigkeit nach seinem Masterabschluss musste er sich oft schnell in die Probleme einarbeiten und konnte nicht so gründlich, sein wie er es aus der Studienzeit gewohnt war. Er beschäftigte sich mit der Optimierung am Einlasskanal in einem Motor mit Hilfe von Strömungsrechnung (CFD). D.h. er hatte sein ursprüngliches Traumziel eigentlich erreicht. Trotzdem war es ihm dann zu viel Routine und er wollte noch mehr über ein Zukunftsthema für Autos lernen: konkret über Batterien. Das kann er nun während der Promotion im Rahmen von SiMET tun. Hier ist er wieder in einem Umfeld von anderen jungen Menschen, die sehr unterschiedliche Masterabschlüsse erworben haben und Mathematik, Computer und die Anwendungsthemen alle verstehen müssen. PODCASTS __ __

41m

Aug 20, 2022

Gudrun hatte 2018 mit Carla Cederbaum https://uni-tuebingen.de/fakultaeten/mathematisch-naturwissenschaftliche-fakultaet/fachbereiche/mathematik/fachbereich/forschung-arbeitsbereiche/geometrische-analysis-differentialgeometrie-und-relativitaetstheorie/personen/prof-dr-carla-cederbaum/ über mathematische Konzepte gesprochen http://modellansatz.de/sternenschwerpunkt, mit denen man z.B. den Schwerpunkt von Sternen bestimmen kann. Im April 2022 trafen sich beide erneut zum Gespräch - diesmal per Videokonferenz. Carla ist inzwischen Professorin an der Uni Tübingen in der AG Geometrische Analysis, Differentialgeometrie und Relativitätstheorie und erhielt den Tübinger Preis für Wissenschaftskommunikation des Jahres 2022. Seit 2021 arbeiten Gudrun und Carla zusammen bei der Gestaltung der Zeitschrift Mitteilungen der Deutschen Mathematiker Vereinigung https://www.degruyter.com/journal/key/dmvm/html?lang=de (MDMV). Gudrun ist 2021-24 als Herausgeberin verantwortlich für die Inhalte und hat neben drei anderen Kolleginnen und Kollegen auch Carla als Mitherausgeberin gewonnen. Im Gespräch geht es um das Praxishandbuch zum Mentoring von Frauen in der mathematischen Forschung https://mentoring.spp2026.de/, das unter der Creative Commons Lizenz CC-BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0/ allen Interessierten zur Verfügung steht und an dessen Weiterentwicklung (auch aufgrund der offenen Lizenz) alle mitarbeiten können. Das Handbuch wurde von Carla Cederbaum, Sophia Jahns und Anna Wienhard https://www.mathi.uni-heidelberg.de/~wienhard/ im Rahmen des Schwerpunktprogramms SPP2026 Geometrie im Unendlichen https://www.spp2026.de/ der Deutschen Forschungsgemeinschaft (DFG) verfasst und basiert auf den Erfahrungen mit dem Math Ment♀ring Programm an der Universität Tübingen unter der Leitung von Carla einerseits und dem UPSTREAM Mentoring Netzwerk an der Universität Heidelberg unter der Leitung von Anna (und Michael Winckler) andererseits. (*) Mentoring gibt es heutzutage in vielen Zusammenhängen und kann konkret sehr viel Unterschiedliches bedeuten. Die Idee, ein spezielles Mentoring für Frauen an ihrem Fachbereich in Tübingen anzubieten, erwuchs aus Carlas eigenen Erfahrungen. Seit ihrem Studium in Freiburg erlebte sie, wie die Tatsache, einer Minderheit im Fach anzugehören, Frauen auf vielfältige Weise dabei behindert, sich in der Mathematik kompetent und in der Fachkultur heimisch zu fühlen. Inzwischen ist gut mit konkreten Zahlen belegt, dass beim Übergang von jeder Entwicklungsstufe auf die nächste in der akademischen Laufbahn mehr Frauen als Männer das Fach verlassen. D.h. bei jedem Karriereschritt sinkt der Anteil von Frauen. So gehen Talente verloren und das Fach Mathematik verliert als Ganzes. In vielen Universitäten hat man das inzwischen als Problem erkannt, dem man strukturell begegnen möchte, aber es gibt oft eine gewisse Ratlosigkeit, wie das geschehen kann. Carla und ihre Mitstreiterinnen sehen als einen Baustein in der Lösung dieses Problems die Wichtigkeit des Austauschs unter Frauen in einem geschützten Rahmen. Dies ist ein effektiver und vergleichsweise kostengünsitger Ansatz. Es geht nicht darum, Frauen zu einer Karriere in der Mathematik zu überreden, sondern diejenigen zu finden und zu unterstützen, die Lust und Talent dazu haben. Unterschiedliche Ausgangssituationen und fehlende Privilegien können so abgemildert werden. An der Duke University baute Carla erstmals Mentoring von und für Frauen in der Mathematik auf, u.a. mit Ingrid Daubechies https://de.wikipedia.org/wiki/Ingrid_Daubechies. Für Tübingen hat sie daraus das Format übernommen, dass die Mentorin der Mentee in der Regel eine Stufe in der Karriereleiter voraus ist. So kann man sich noch recht einfach hineindenken, wie man selbst noch vor kurzem gedacht und gearbeitet hat - außerdem ist es ideal, wenn man selbst als Mentee in einem weiteren "Gespann" die "andere Seite" des Mentorings erlebt. In jedem Fall ist es hilfreich, wenn Mentorinnen eine Schulung oder zumindest eine Handreichung bekommen, bevor sie diese Rolle übernehmen. Im Handbuch ist erprobtes Material für die Schulung der Mentorinnen zusammengetragen (inkl. aller möglicher Vorlagen für Anschreiben, Aushänge etc.). Eine ausführliche und weiter wachsende Literatursammlung zu Mentoring und Gender Studies rundet das Material ab. Die grundlegende Struktur des Mentorings ruht außerdem auf folgenden Prinzipien: __ __ In Tübingen dauert die Mentorinnenschulung 1/2 Tag und konzentriert sich auf die Frage: Was ist Mentoring und was nicht und wie kann ich das konkret gestalten. In einem ersten Teil der Schulung werden typische Argumente und belegte Fakten erörtert, die für und gegen die Notwendigkeit der Unterstützung von Frauen in der Mathematik sprechen. Dafür hat sich das Format der Fishbowl-Diskussion zwischen zwei ausgelosten Gruppen bewährt. Danach werden offenes und proaktives Zuhören geübt und Antworten auf typische Mentoringfragen in unterschiedlichen Karrierestufen gesammelt. Das geschieht in 3er-Gruppen mit den Rollen Mentee/Mentorin/Beobachterin. Jede Gruppe zieht zufällig eine Vignette und spielt ein Gespräch zur dort geschilderten Situation durch. Anschließend erfolgt jeweils eine Besprechung dazu, wie die Personen die Gespräche in den unterschiedlichen Rollen wahrgenommen haben, was gut funktioniert hat und was vielleicht nicht so gut gelaufen ist. Danach werden die Rollen getauscht. Schließlich wird im dritten Teil der Schulung das erste Treffen mit einer Mentee vorbereitet, um eventuelle Nervosität oder Anspannung abzubauen. Man arbeitet in Paaren, um sich das erste Treffen möglichst genau vorzustellen. Hierbei werden die Paare von Schlüsselfragen geleitet. Auch werden Anlaufstellen für über das Mentoring hinausgehende Fragestellungen vorgestellt. Im Handbuch sind zu allen Teilen der Schulung viele Fallbeispiele und Schlüsselfragen gesammelt. Daneben finden sich Vorlagen für Werbung, Organisatorisches zu Treffen und zur Kontaktaufnahme. Es sind aber auch Verweise auf Ressourcen gesammelt, falls es ernsthafte Probleme gibt, die im Mentoringgespräch nicht gelöst werden können (wie z.B. Prüfungsangst, finanzielle Sorgen oder eine psychische Krise). Es wird dafür sensibilisiert, wie man erkennen kann, für welche Fragen man selbst eine kompetente Ansprechperson ist und dass es im Mentoring nicht darum geht ein "Mini-me" zu erziehen - nicht alles was für mich funktioniert hat, ist auch für das Gegenüber gut. Deshalb ist es wichtig, die Werte des Gegenübers herausfinden und dann die Zielsetzung der gemeinsamen Zeit möglichst danach auszurichten. Das Mentoring in Tübingen hat 2014/15 begonnen - der Übergang zur Postdoc-Phase scheint vor Ort das größte Leck zu sein. Als Gründe nennen die Mentees, dass eine akademische Laufbahn sich schwer mit Familiengründung und Partnerschaft vertrage, wenn in der Postdoc-Phase 2-3 längere Auslansdaufenthalte oder wenigstens Wechsel zwischen deutschen Universitäten erwartet werden. Gudrun hat für den Podcast mit drei Frauen gesprochen, die in Tübingen am Mentoringprogramm teilgenommen haben und inzwischen auf der nächsten Karrierestufe arbeiten. Das Gespräch mit Polyxeni Spiloti ist schon veröffentlicht. Die Gespräche mit Cornelia Vogel und Alix Richter folgen bald. Cornelia und Alix waren als Studentinnen Mentees und haben sich jeweils für eine Promotion entschieden, an der sie zur Zeit des Gespräches in Tübingen bzw. Paderborn arbeiteten. (*) Zusätzliche Förderung erhielt das Projekt durch die Duke University, das Zukunftskonzept der Universität Tübingen (DFG, ZUK 63) und durch das Athene-Mentoring Programm, Universität Tübingen, die HGS MathComp https://www.mathcomp.uni-heidelberg.de/home am IWR Heidelberg, den Exzellenzcluster STRUCTURES und die Research Station Geometry & Dynamics der Universität Heidelberg. * REFERENZEN UND WEITERE INFORMATIONEN __ __ * PODCASTS __ __

34m

Jul 28, 2022

Gudrun talks with Polyxeni Spilioti https://www.polyxenispilioti.com/ at Aarhus university https://international.au.dk/ about spectral geometry https://en.wikipedia.org/wiki/Spectral_geometry. Before working in Aarhus Polyxeni was a postdoctoral researcher in the group of Anton Deitmar at the University of Tübingen. She received her PhD from the University of Bonn, under the supervision of Werner Mueller after earning her Master's at the National and Technical University of Athens (Faculty of Applied Mathematics and Physics). As postdoc she was also guest at the MPI for Mathematics in Bonn https://www.mpim-bonn.mpg.de/en, the Institut des Hautes Etudes Scientifiques https://www.ihes.fr/en/ in Paris and the Oberwolfach Research Institute for Mathematics https://www.mfo.de/. In her research she works on questions like: How can one obtain information about the geometry of a manifold https://en.wikipedia.org/wiki/Manifold, such as the volume, the curvature, or the length of the closed geodesics https://en.wikipedia.org/wiki/Geodesic, provided that we can study the spectrum of certain differential operators? Harmonic analysis on locally symmetric spaces provides a powerful machinery in studying various invariants, such as the analytic torsion https://en.wikipedia.org/wiki/Analytic_torsion, as well as the dynamical zeta functions https://en.wikipedia.org/wiki/Ruelle_zeta_function of Ruelle and Selberg. * REFERENCES AND FURTHER INFORMATION __ __ * PODCASTS __ __

40m

Jun 01, 2022

Gudrun spricht in dieser Folge mit Ute Badde in der Landesanstalt für Umwelt Baden-Württemberg (LUBW) https://www.lubw.baden-wuerttemberg.de/die-lubw am Südende von Karlsruhe. Am 3. Februar, hatte Gudrun mit der Vorlesung Mathematical Modelling and Simulation eine Exkursion in die LUBW unternommen. Geplant war, den Studierenden zu zeigen, wie dort Modelle und Simulationen der Wasserläufe in Karlsruhe eingesetzt werden und mit den Wettervorhersagen als Eingangsdaten arbeiten. Zufällig war es so, dass an diesem Tag eine recht massive Hochwasserlage herrschte. Und zwar nicht aufgrund von außergewöhnlichen oder überraschend heftigen Niederschlägen, sondern aufgrund eines mehrstündigen Landregens. Tatsächlich hätte aufgrund der außerdem noch ungewöhnlich hohen Temperatur noch mehr Wasser unterwegs sein können, wenn auch noch Tauwasser aus den Bergen hinzugekommen wäre. Da es aber in dem Winter zuvor kaum Schnee gegeben hatte, war der Regen der wesentliche Wassereintrag, Jedenfalls war die eigentliche Hochwasserzentrale am Tag der Exkursion besetzt und die Gruppe wich in einen anderen Raum aus. Zum aktuellen Hochwassergeschehen konnte sie aber sehr eindrückliche Informationen mitnehmen. Hochwasser war dann auch ein Thema im späten Frühjahr und in den Sommermonaten 2021. Es gab einige Starkregenereignisse mit Überschwemmungen südlich von Stuttgart und der Rhein war lange Wochen nicht schiffbar und es gab einige Perioden, wo der Auenwald am Rhein überflutet war. Dieses Geschehen in Baden-Württemberg im Auge zu haben und zwar in der Messung und für kurzzeitige und mittelfristige Prognosen ist die Aufgabe der Arbeitsgruppe von Ute Badde an der LUBW. Als Bürger hat man auf diese Daten z.B. Zugriff über die Seiten der Hochwasservorhersage in Baden-Württemberg https://www.hvz.baden-wuerttemberg.de/. Dafür gibt es Zugang zu Messdaten (z.B. Pegelstände) zu unterschiedlichen meteorologischen Modellen und zu einer Armee leistungsstarker Rechner, die dann aus den Daten und den Wettervorhersagen eine Prognose für die Wasserstände der Flüsse wie Rhein, Neckar oder auch den Bodensee berechnen. Damit ist es dann möglich, wenn es brenzlig wird, Gemeinden und Gewerbetreibende zu beraten ob und wenn ja welche Vorsorge vor Ort getroffen werden sollte. Ute hat Bauingenieurwesen am KIT studiert und sich anschließend in der Hydrologie spezialisiert. In die LUBW ist sie zunächst auf einer Projektstelle eingestiegen. Inzwischen hat sie dort eine feste Stelle. Ihr gefällt nach wie vor sehr gut, dass sie an der Schnittstelle von Computern und Modellen ganz Praxis-relevante Fragen beantworten kann und insbesodere in Extremsituationen Entscheidungshilfen geben kann. Außerdem ist es eine schöne Herausforderung, über ihre Arbeit zu berichten. Oft für Zeitungen und das lokale Fernsehen aber diesmal auch im Podcast. * REFERENZEN UND WEITERFÜHRENDE INFORMATIONEN __ __ * PODCASTS __ __

26m

Mar 17, 2022

One of the reasons we started this podcast in 2013 was to provide a more realistic picture of mathematics and of the way mathematicians work. On Nov. 19 2021 Gudrun talked to Stephanie Anne Salomone who is Professor and Chair in Mathematics at the University of Portland https://www.up.edu/. She is also Director of the STEM Education and Outreach Center and Faculty Athletic Representative at UP. She is an Associate Director of Project NExT, a program of the Mathematical Association of America that provides networking and professional development opportunities to mathematics faculty who are new to our profession. She is a wife and mother of three boys, Milo (13), Jude (10), and Theodore (8). This conversation started on Twitter in the summer of 2021. There Stephanie (under the twitter handle @SitDownPee https://twitter.com/sitdownpee) and @stanyoshinobu https://twitter.com/stanyoshinobu Dr. Stan Yoshinobu invited their fellow mathematicians to the following workshop: Come help us build gender equity in mathematics! Picture a Mathematician workshop led by @stanyoshinobu Dr. Stan Yoshinobu and me, designed for men in math, but all genders welcome. Gudrun was curious to learn more and followed the provided link: Workshop Abstract http://www.inquirybasedlearning.org/pam Gender equity in the mathematical sciences and in the academy broadly is not yet a reality. Women (and people of color, and other historically excluded groups) are confronted with systemic biases, daily experiences, feelings of not being welcome or included, that in the aggregate push them out of the mathematical sciences. This workshop is designed primarily for men in math (although all genders are welcome to participate) to inform and inspire them to better see some of the key issues with empathy, and then to take action in creating a level-playing field in the academy. Workshop activities include viewing “Picture a Scientist” before the workshop, a 2-hour synchronous workshop via zoom, and follow-up discussions via email and Discord server. *All genders welcome AND this workshop is designed for men to be allies. This idea resonated strongly with Gudrun's experiences: Of course women and other groups which are minorities in research have to speak out to fight for their place but things move forward only if people with power join the cause. At the moment people with power in mathematical research mostly means white men. That is true for the US where Stephanie is working as well as in Germany. Allyship https://en.wikipedia.org/wiki/Allyship is a concept which was introduced by people of colour to name white people fighting for racial justice at their side. Of course, it is a concept which helps in all situations where a group is less powerful than another. Men working for the advancement of non-male mathematicians is strictly necessary in order for equality of chances and a diversity of people in mathematics to be achieved in the next generation. And to be clear: this has nothing to do with counting heads but it is about not ruining the future of mathematics as a discipline by creating obstacles for mathematicians with minoritized identities. The important question is: How is it possible to educate men and especially powerful white men to become allies? The idea of this first workshop designed by Stephanie and Stan was to invite men already interested in learning more and to build a basis with the documentary Picture a scientist https://www.pictureascientist.com/ (2020). * SYNOPSIS PICTURE A SCIENTIST chronicles the groundswell of researchers who are writing a new chapter for women scientists. Biologist Nancy Hopkins, chemist Raychelle Burks, and geologist Jane Willenbring lead viewers on a journey deep into their own experiences in the sciences, ranging from brutal harassment to years of subtle slights. Along the way, from cramped laboratories to spectacular field stations, we encounter scientific luminaries - including social scientists, neuroscientists, and psychologists - who provide new perspectives on how to make science itself more diverse, equitable, and open to all. (from the webpage) In this film there are no mathematicians, but the situations in sciences and mathematics are very similar and for that it lends itself to show the situation. In the podcast conversation Gudrun and Stephanie talk about why and in what way the documentary spoke to them. The huge and small obstacles in their own work as women mathematicians which do not make them feel welcome in a field they feel passionate about. The film shows what happens to women in Science. It shows also men in different roles. Obviously there are the bullies. Then there are the bystanders. There are universities which allow women to be hired and give them the smallest space available. But there are also men who consider themselves friends of their female collaegues who cannot believe that they did not notice how the behaviour of other men (and their own behavior in not taking a side). Seeing this play out over the course of the film is not a comfortable watch, and perhaps because of this discomfort, we hope to build empathy. On the other hand, there is a story of women scientists who noticed that they were not treated as well as their male colleagues and who found each other to fight for office space and the recognition of their work. They succeded a generation ago. The general idea of the workshop was to start with the documentary and to talk about different people and their role in the film in order to take them as prototypical for roles which we happen to observe in our life and which we might happen to play. This discussion in groups was moderated and guided in order to make this a safe space for everyone. Stephanie spoke about how we have to let men grow into their responsibility to speak out against a hostile atmosphere at university created mostly by men. In the workshop it was possible to first develop and then train for possible responses in situations which ask for men stepping in as an ally. The next iteration of the workshop Picture a Mathematician will be on May 11. Biography: Stephanie Salomone earned her Ph.D. in Mathematics from UCLA in 2005 and joined the faculty at the University of Portland that year. She serves as Professor and Chair of Mathematics and Director of the STEM Education and Outreach Center at UP, as well as the Faculty Athletic Representative. She is an Associate Director of Project NExT, a national professional development program for new higher-education mathematics faculty. She was the PI on the NSF REFLECT program, advancing the use of evidence-based practices in STEM teaching at UP and the use of peer-observation for formative assessment of teaching, and has managed a combined $1.6 million as the PI on a subaward of the Western Regional Noyce Alliance grant and as PI of the NSF Noyce Program at UP. She is on the Board of Directors for Saturday Academy, a local 501c3 whose mission is to engage children in hands-on STEM learning. Dr. Salomone is the recipient of UP’s 2009 Outstanding Teaching Award and the recipient of the 2019 Oregon Academy of Sciences Outstanding Educator in STEM Higher Education Award. * LITERATURE AND FURTHER INFORMATION __ __ Science 368, Issue 6497, 1317-1319 (2020). https://doi.org/10.1126/science.aba7377 __ __ * PODCASTS __ __

53m

Jan 27, 2022

Gudrun spricht in dieser Folge mit Pauline Brumm https://www.sfb1194.tu-darmstadt.de/sfb_1194/kontakt_9/detailseite_sfb1194_166400.de.jsp von der TU Darmstadt https://www.tu-darmstadt.de/ über Benetzung im Tiefdruck. Sie ist wissenschaftliche Mitarbeiterin am Institut für Druckmaschinen und Druckverfahren https://www.idd.tu-darmstadt.de/idd/index.de.jsp und promoviert im SFB 1194 zur Mechanischen Zwangsbenetzung von Oberflächen durch gravierte Tiefdruckzylinder https://www.sfb1194.tu-darmstadt.de/forschung_13/projektbereiche/bereich_c/c01_tiefdruckzylinder/index.de.jsp im Teilprojekt C01. Es handelt sich um eine Weiterführung des Gesprächs mit Dr. Mathis Fricke im Modellansatz-Podcast Folge 242 http://modellansatz.de/dynamische-benetzung über Dynamische Benetzung. Herr Fricke hatte über die Arbeit im SFB 1194 aus Sicht der Mathematik berichtet, Frau Brumm liefert in dieser Folge nun einen Beitrag aus Sicht der Anwendung. Sie hat Maschinenbau im Bachelor und Master an der TU Darmstadt studiert und sich auf Drucktechnik spezialisiert. Drucken wird seit hunderten von Jahren praktiziert und angewendet, jedoch gibt es bisher noch keine umfassende Modellbildung für viele Druckprozesse. Das bedeutet, dass ein Großteil des Wissens empirisch geprägt ist. Firmen stützen sich auf die Erfahrung von gelernten Drucktechnikern, jedoch ist diese Erfahrung nur selten öffentlich zugänglich und es gibt wenige Forschungsinstitute weltweit zum Thema Drucktechnik. Um innovative Anwendungen zu entwickeln, zum Beispiel aus dem Bereich der gedruckten Elektronik, bedarf es jedoch einer detaillierten Modellvorstellung des Druckprozesses, um klassische Druckverfahren aus dem grafischen Druck (Zeitungsdruck, Verpackungsdruck etc.) für den sogenannten „funktionalen Druck“ nutzbar zu machen. Die Schwierigkeit liegt darin, dass an den funktionalen Druck ganz andere Anforderungen gestellt werden, zum Beispiel müssen die gedruckten, häufig ultradünnen Schichten geschlossen, fehlerfrei und von konstanter Schichtdicke sein. Ein häufiger Druckfehler ist das sogenannte „Viscous Fingering“, eine hochdynamische Grenzflächeninstabilität bei der Fluidübertragung, die sich in Form von faszinierenden, verästelten, fingerartigen Strukturen in der gedruckten Schicht bemerkbar macht. Sie sehen so ähnlich aus wie die Arme eines Flussdeltas aus Vogelperspektive oder die Wurzeln von Bäumen. In ihrer Forschung untersucht Frau Brumm diese verästelten Strukturen im Tiefdruck, um sie besser zu verstehen und um den Druckfehler in Zukunft zu verhindern oder für spezielle Anwendungen nutzbar zu machen. Beim Tiefdruck wird die Farbe über gravierte Näpfchen in einem Druckzylinder übertragen. Die Näpfchen liegen vertieft und sind nur wenige zehn Mikrometer groß. Beim Kontakt mit dem zu bedruckenden Substrat (Papier, Folie, Glas…) wird die Druckfarbe unter hohem Druck und hoher Geschwindigkeit aus den Näpfchen herausgesaugt. Es kommt zur Zwangsbenetzung des Substrats. Mit Stokes-Gleichungen kann man Parametermodelle herleiten, welche das Skalierungsverhalten der verästelten, gedruckten Strukturen beschreiben. Zum Beispiel skaliert der dominante Abstand der gedruckten Strukturen mit der Druckgeschwindigkeit hoch minus ein Halb laut Sauer et al. (2015) https://iarigai.com/download/683/, welches dem 60 Jahre alten Skalengesetz von Saffman und Taylor (1958) https://doi.org/10.1098/rspa.1958.0085 entspricht. Mit Experimenten können diese Modelle bestätigt oder widerlegt werden. Die Planung von Experimenten geschieht zielgerichtet. Im Vorfeld muss überlegt werden, welche Parameter im Experiment variiert werden sollen und wie viele Messpunkte benötigt werden, um statistisch abgesicherte Aussagen treffen zu können. Meistens ist die Herausforderung, die Vielzahl der Parameterkombinationen auf ein Minimum zu reduzieren und dennoch die gewünschten Aussagen treffen zu können. Die gedruckten Proben werden hochauflösend mit einem Flachbettscanner digitalisiert und danach werden Bildverarbeitungsmethoden in den ingenieurstypischen Programmiersprachen Matlab oder Python angewendet. Beispielsweise wird eine Fast Fourier Transformation https://de.wikipedia.org/wiki/Schnelle_Fourier-Transformation (FFT) benutzt, um den dominanten Abstand der gedruckten Strukturen zu ermitteln. Die Automatisierung des Experiments und vor allem der anschließenden Auswertung ist ein weiterer wichtiger Punkt. Um zehntausende von gedruckten Mustern zu analysieren, wurde ein hochautomatisierter computergestützter Workflow entwickelt. Seit kurzem wird von Frau Brumm auch Künstliche Intelligenz, genauer gesagt Deep Learning https://de.wikipedia.org/wiki/Deep_Learning, zur Klassifizierung der gedruckten Muster verwendet. Dies ist notwendig, um die Skalierbarkeit hin zu industriellen Prozessen zu ermöglichen, indem umfangreiche Versuchsreihen an industriellen Maschinen durchgeführt und automatisiert ausgewertet werden. Diese werden anschließend mit kleineren Versuchsreihen an speziell entwickelten Labormaschinen verglichen, bei denen teilweise auch Modellfluide anstelle von realen Druckfarben verwendet werden. Bei Laborexperimenten werden in Teilprojekt C01 im SFB 1194 auch Hochgeschwindigkeitsvideos der hochdynamischen Grenzflächeninstabilität aufgenommen, die noch tiefere Einblicke in die Strömungsdynamik bieten und die industriellen Experimente ergänzen und erklären sollen. Der Maschinenbau ist sehr breit gefächert und das Studium muss dementsprechend auch breite Kenntnisse vermitteln. Beispielsweise werden umfangreiche Methoden aus der Mathematik gelehrt, damit ein/e Maschinenbau-Absolvent/in für die diversen Anwendungsaufgaben gerüstet ist. In der modernen Forschung ist die Fähigkeit zur interdisziplinären Zusammenarbeit und zur Wissenschaftskommunikation sehr entscheidend. Maschinenbauer/innen im SFB 1194 arbeiten beispielsweise mit Mathematikern/innen, Physikern/innen und Informatikern/innen zusammen, um eine größere Forschungsfrage zu beantworten. In dieser Podcast-Folge wird auch an junge Frauen appelliert, ein MINT-Studium auszuprobieren, um mehr Diversität im Studium, Forschung und Industrie zu erreichen, um am Ende noch innovativere Lösungen zu schaffen, die der Welt einen Nutzen bringen. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

49m

Dec 24, 2021

Gudrun spricht in dieser Folge mit Sarah Bischof, Timo Bohlig und Jonas Albrecht. Die drei haben im Sommersemester 2021 am Projektorientiertes Softwarepraktikum https://www.lbrg.kit.edu/page/projsoftpr teilgenommen. Das Praktikum wurde 2010 als forschungsnaher Lernort konzipiert. Studierende unterschiedlicher Studiengänge arbeiten dort ein Semester lang an konkreten Strömungssimulationen. Es wird regelmäßig im Sommersemester angeboten. Seit 2014 liegt als Programmiersprache die Open Source Software OpenLB https://www.openlb.net/ zugrunde, die ständig u.a. in der Karlsruher Lattice Boltzmann Research Group (LBRG) https://www.lbrg.kit.edu/ weiter entwickelt wird. Konkret läuft das Praktikum etwa folgendermaßen ab: Die Studierenden erhalten eine theoretische Einführung in Strömungsmodelle, die Idee von Lattice-Boltzmann-Methoden und die Nutzung der Hochleistungrechner am KIT. Außerdem finden sie sich für ein einführendes kleines Projekt in Gruppen zusammen. Anschließend wählen sie aus einem Katalog eine Frage aus, die sie bis zum Ende des Semesters mit Hilfe von Computersimulationen gemeinsam beantworten. Diese Fragen sind Teile von Forschungsthemen der Gruppe, z.B. aus Promotionsprojekten oder Drittmittelforschung. Während der Projektphase werden die Studierenden von dem Doktoranden/der Doktorandin der Gruppe, die die jeweilige Frage gestellt haben, betreut. Am Ende des Semesters werden die Ergebnisse in Vorträgen vorgestellt und diskutiert oder es wird eine Podcastfolge aufgenommen. In einer Ausarbeitung werden außerdem die Modellbildung, die Umsetzung in OpenLB und die konkreten Simulationsergebnisse ausführlich dargelegt und in den aktuellen Forschungsstand eingeordnet. Sarah, Timo und Jonas sind am KIT im Masterstudiengang Chemieingenieurwesen https://www.ciw.kit.edu/1629.php eingeschrieben. Neben den verschiedenen Masterstudiengängen Mathematik kommen aus diesem Studiengang die meisten Interessenten für das Softwarepraktikum. Im Podcast erläutern sie, was sie an der Strömungssimulation interessiert und inwieweit sie sich gut oder auch nicht so gut auf die Anforderungen vorbereitet gefühlt haben, wie sie sich die Arbeit in der Gruppe aufgeteilt haben und was sie an fachlichen und überfachlichen Dingen dort gelernt haben. Das Thema des Projektes war ein Benchmark https://de.wikipedia.org/wiki/Benchmark für die Durchströmung der Aorta https://de.wikipedia.org/wiki/Aorta. Dies ist einer der Showcases für OpenLB, die auf den ersten Blick die Leistungsfähigkeit der Software demonstrieren sollen. Das Projekt wurde von der Gruppe in drei Teile gegliedert: __ __ Mit Hilfe der Benchmark Tests auf dem HPC konnte die maximale Skalierbarkeit des Aorta Source Codes in Abhängigkeit der Problemgröße gefunden werden. Sie gibt an, auf wie vielen Computerprozessoren der Showcase mit der höchsten Performance simuliert werden kann. Des Weiteren wurde die parallele Effizienz mit Hilfe der Speedup https://de.wikipedia.org/wiki/Speedup Kennzahl untersucht. Diese beschreibt inwiefern sich die Simulationszeit infolge von Erhöhung der Prozessoranzahl verringert. In beiden Fällen zeigten die Performanceindikatoren ein Maximum bei 400-700 Prozessoreinheiten für Problemgrößen bis zu einer Resolution von N = 80. Das Softwarepaket OpenLB beinhaltet in Release 1.4r0 keine detaillierten Schnittstellen zur Performancemessung. Durch eine Source Code Erweiterung konnte eine interne Zeitmessung der einzelnen Funktionen des Codes realisiert werden. Dabei wurden so genannte Bottlenecks https://en.wikipedia.org/wiki/Bottleneck_(software) identifiziert und dokumentiert, welche durch Updates in zukünftigen Versionen der Software eliminiert werden sollen. Des Weiteren konnte auch durch die Code Erweiterung eine Aussage über die Parallelisierung getroffen werden. Im Vergleich zu den Benchmark Tests können direkt Funktionen des Source Codes, die die Parallelisierung hemmen, bestimmt werden. Die Performance Analyse durch das externe Programm und durch die Source Code Erweiterung bestätigen eine gut funktionierende Parallelisierung. Die Realisierung erfolgte dabei durch die Messung der Laufzeit der Hauptschritte einer OpenLB Simulation, sowie der detaillierten Analyse einzelner Funktionen. Diese finden sich zum aktuellen Zeitpunkt im Post-Processing des "Collide And Stream" Schrittes der Simulation. Collide And Stream beschreibt einen lokalen Berechnungsschritt, einen lokalen und einen nicht lokalen Übertragungsschritt. Der Kollisionsschritt bestimmt ein lokales Gleichgewicht der Massen-, Momenten- und Energiebilanzen. Im nicht-lokalen Streaming Schritt werden diese Werte auf die angrenzenden Blöcke des Simulationsgitters übertragen. Dies ermöglicht im Vergleich zu CFD-Simulationen, die auf Basis der Finite-Volumen-Methode https://de.wikipedia.org/wiki/Finite-Volumen-Verfahren (FVM) die Navier-Stokes Gleichungen https://de.wikipedia.org/wiki/Navier-Stokes-Gleichungen lösen, effizientere Parallelisierung insbesondere bei Einsatz einer HPC-Einheit. Die Post Prozessoren im Collide And Stream wenden unter anderem bestimmte, im vorangegangenen Schritt gesetzte Randbedingungen auf definierte Bereiche der Simulationsgeometrie an. Sie werden dabei nur für nicht-lokale Randbedingungen verwendet, weitere Randbedingungen können auch innerhalb des Kollisionsschrittes modelliert werden. Im Showcase der Aorta ist für das Fluid (Blut) am Eingang der Simulation eine Geschwindigkeits-Randbedingung nach Bouzidi mit Poiseuille-Strömungsprofil und am Ausgang eine "stress-free" Bedingung gewählt. Für die Aortawand ist eine no-slip Bedingung mit Fluidgeschwindigkeit null implementiert (Für genauere Informationen zum Simulationsaufbau hier https://link.springer.com/chapter/10.1007%2F978-3-642-36961-2_5 und hier https://doi.org/10.1002/jmri.25366. Die Laufzeit der Post-Processor Funktionen, deren Aufgabe es ist die Randbedingungen anzuwenden, können mit dem Timer des Release 1.4r0 nicht analysiert werden. Mit Blick auf spätere Releases ist es mit der Source Code Erweiterung nun möglich mit geringem Aufwand Daten über die Effizienz der vorhandenen, neuer oder verbesserter Funktionen in OpenLB zu gewinnen. Eine integrierte Zeitmessung als Analysetool kann einen direkten Einfluss auf die Performance des Source Codes haben, weshalb mit Hilfe der externen Software AMDµProf http://developer.amd.com/wordpress/media/2013/12/AMDuprof-User_Guide.pdf die Bottlenecks validiert wurden. Sowohl bei der internen als auch externe Performance Analyse sind die selben Post-Processing Schritte als Bottlenecks erkennbar, welches die Code Erweiterung validiert. Zusätzlich konnte mit der AMDμProf-Software die aktuelle OpenLB Version 1.4r0 mit der vorherigen Version 1.3r1 verglichen werden. Dabei fällt auf, dass sich die Bottlenecks vom Berechnungsschritt in Collide And Stream (Release 1.3r1) zum Post-Processing Schritt in Collide And Stream (Release 1.4r0) verschoben haben. Abschließend wurde eine vektorisierte Version von OpenLB erfolgreich getestet und ebenfalls auf Bottlenecks untersucht. Eine Vektorisierung eines Codes, auch bekannt als SIMD https://de.wikipedia.org/wiki/Flynnsche_Klassifikation#SIMD_(Single_Instruction,_Multiple_Data), soll die Parallelisierung verbessern und der Aorta Simulation eine bessere Performance verleihen. Das Bottleneck des Post-Processing Schritts in Collide And Stream, speziell durch Implementierung neuer Bouzidi Boundaries, wurde durch eine weitere Gruppe im Rahmen des Projektorientierten Softwarepraktikums optimiert. Es konnte eine Performance Verbesserung um einen Faktor 3 erreicht werden (mit OpenMP Compiler). Durch eine gezielte Analyse der Bottlenecks im Code konnte das Potential für die Beschleunigung der Simulation erweitert werden. Aber natürlich lohnt es sich hier weiterhin anzusehen, wo noch konkretes Potential für die Beschleunigung der Simulation liegt. Zumal seit dem letzten Relounch einige Pardigmen in der Software OpenLB verändert wurden. * PODCASTS __ __ * LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __

34m

Aug 20, 2021

Gudrun spricht in dieser Folge mit Mathis Fricke https://www.mma.tu-darmstadt.de/index/mitarbeiter_3/mitarbeiter_details_mma_48384.en.jsp von der TU Darmstadt https://www.tu-darmstadt.de/ über Dynamische Benetzungsphänomene. Er hat 2020 in der Gruppe Mathematical Modeling and Analysis https://www.mma.tu-darmstadt.de/index/index.en.jsp bei Prof. Dieter Bothe https://www.mma.tu-darmstadt.de/index/mitarbeiter_3/mitarbeiter_details_mma_43073.en.jsp promoviert. Diese Gruppe ist in der Analysis und damit in der Fakultät für Mathematik angesiedelt, arbeitet aber stark interdisziplinär vernetzt, weil dort Probleme aus der Verfahrenstechnik modelliert und simuliert werden. Viele Anwendungen in den Ingenieurwissenschaften erfordern ein tiefes Verständnis der physikalischen Vorgänge in mehrphasigen Strömungen, d.h. Strömungen mit mehreren Komponenten. Eine sog. "Kontaktlinie" entsteht, wenn drei thermodynamische Phasen zusammenkommen und ein komplexes System bilden. Ein typisches Beispiel ist ein Flüssigkeitströpfchen, das auf einer Wand sitzt (oder sich bewegt) und von der Umgebungsluft umgeben ist. Ein wichtiger physikalischer Parameter ist dabei der "Kontaktwinkel" zwischen der Gas/Flüssig-Grenzfläche und der festen Oberfläche. Ist der Kontaktwinkel klein ist die Oberfläche hydrophil (also gut benetzend), ist der Kontaktwinkel groß ist die Oberläche hydrophob (schlecht benetzend). Je nach Anwendungsfall können beide Situationen in der Praxis gewollt sein. Zum Beispiel können stark hydrophobe Oberflächen einen Selbstreinigungseffekt aufweisen weil Wassertropfen von der Oberfläche abrollen und dabei Schmutzpartikel abtransportieren (siehe z.B. https://de.wikipedia.org/wiki/Lotoseffekt). Dynamische Benetzungsphänomene sind in Natur und Technik allgegenwärtig. Die Beine eines Wasserläufers nutzen eine ausgeklügelte hierarchische Oberflächenstruktur, um Superhydrophobie zu erreichen und das Insekt auf einer Wasseroberfläche leicht stehen und laufen zu lassen. Die Fähigkeit, dynamische Benetzungsprozesse zu verstehen und zu steuern, ist entscheidend für eine Vielzahl industrieller und technischer Prozesse wie Bioprinting und Tintenstrahldruck oder Massentransport in Mikrofluidikgeräten. Andererseits birgt das Problem der beweglichen Kontaktlinie selbst in einer stark vereinfachten Formulierung immer noch erhebliche Herausforderungen hinsichtlich der fundamentalen mathematischen Modellierung sowie der numerischen Methoden. Ein übliche Ansatz zur Beschreibung eines Mehrphasensystems auf einer makroskopischen Skala ist die Kontinuumsphysik, bei der die mikroskopische Struktur der Materie nicht explizit aufgelöst wird. Andererseits finden die physikalischen Prozesse an der Kontaktlinie auf einer sehr kleinen Längenskala statt. Man muss daher das Standardmodell der Kontinuumsphysik erweitern, um zu einer korrekten Beschreibung des Systems zu gelangen. Ein wichtiges Leitprinzip bei der mathematischen Modellierung ist dabei der zweite Hauptsatz der Thermodynamik, der besagt, dass die Entropie eines isolierten Systems niemals abnimmt. Dieses tiefe physikalische Prinzip hilft, zu einem geschlossenen und zuverlässigen Modell zu kommen. Die größte Herausforderung in der kontinuumsmechanischen Modellierung von dynamischen Benetzungsprozessen ist die Formulierung der Randbedingungen für die Navier Stokes Gleichungen an der Festkörperoberfläche sowie am freien Rand zwischen Gas und Flüssigkeit. Die klassische Arbeit von Huh und Scriven hat gezeigt, dass die übliche Haftbedingung ("no slip") an der Festkörperoberfläche nicht mit einer bewegten Kontaktlinie und damit mit einem dynamischen Benetzungsprozess verträglich ist. Man kann nämlich leicht zeigen, dass die Lösung für die Geschwindigkeit in diesem Fall unstetig an der Kontaktlinie wäre. Weil das Fluid (z.B. Wasser) aber eine innere Reibung (Viskosität) besitzt, würde dann mit einer unendlichen Rate ("singulär") innere Energie in Wärme umgewandelt ("dissipiert"). Dieses Verhalten ist offensichtlich unphysikalisch und zeigt dass eine Anpassung des Modells nötig ist. Einer der wesentlichen Beiträge von Mathis Dissertation ist die qualitative Analyse von solchen angepassten Modellen (zur Vermeidung der unphysikalischen Singularität) mit Methoden aus der Geometrie. Die Idee ist hierbei eine systematische Untersuchung der "Kinematik", d.h. der Geometrie der Bewegung der Kontaktlinie und des Kontaktwinkels. Nimmt man das transportierende Geschwindigkeitsfeld als gegeben an, so kann man einen fundamentalen geometrischen Zusammenhang zwischen der Änderungsrate des Kontaktwinkels und der Struktur des Geschwindigkeitsfeldes herleiten. Dieser geometrische (bzw. kinematische) Zusammenhang gilt universell für alle Modelle (in der betrachteten Modellklasse) und erlaubt tiefe Einsichten in das qualitative Verhalten von Lösungen. Neben der mathematischen Modellierung braucht man auch numerische Werkzeuge und Algorithmen zur Lösung der resultierenden partiellen Differentialgleichungen, die typischerweise eine Variante der bekannten Navier-Stokes-Gleichungen sind. Diese nichtlinearen PDE-Modelle erfordern eine sorgfältige Auswahl der numerischen Methoden und einen hohen Rechenaufwand. Mathis entschied sich für numerische Methoden auf der Grundlage der geometrischen VOF (Volume-of-Fluid) Methode. Die VOF Methode ist eine Finite Volumen Methode und basiert auf einem diskreten Gitter von würfelförmigen Kontrollvolumen auf dem die Lösung des PDE Systems angenähert wird. Wichtig ist hier insbesondere die Verfolgung der räumlichen Position der freien Grenzfläche und der Kontaktlinie. In der VOF Methode wird dazu für jede Gitterzelle gespeichert zu welchem Anteil sie mit Flüssigkeit bzw. Gas gefüllt ist. Aus dieser Information kann später die Form der freien Grenzfläche rekonstruiert werden. Im Rahmen von Mathis Dissertation wurden diese Rekonstruktionsverfahren hinsichtlich Ihrer Genauigkeit nahe der Kontaktlinie weiterentwickelt. Zusammen mit komplementären numerischen Methoden sowie Experimenten im Sonderforschungsbereich 1194 https://www.sfb1194.tu-darmstadt.de/ können die Methoden in realistischen Testfällen validiert werden. Mathis hat sich in seiner Arbeit vor allem mit der Dynamik des Anstiegs einer Flüssigkeitssäule in einer Kapillare sowie der Aufbruchdynamik von Flüssigkeitsbrücken (sog. "Kapillarbrücken") auf strukturierten Oberflächen beschäftigt. Die Simulation kann hier als eine numerische "Lupe" dienen und Phänomene sichtbar machen die, z.B wegen einer limitierten zeitlichen Auflösung, im Experiment nur schwer sichtbar gemacht werden können. Gleichzeitig werden die experimentellen Daten genutzt um die Korrektheit des Modells und des numerischen Verfahrens zu überprüfen. * LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ 229(10), 1849–1865 (2020). __ __ * PODCASTS __ __

1h 6m

Jul 11, 2021

Gudrun spricht in dieser Folge mit Attila Genda über sein Praktikum bei Dassault Systèmes https://www.3ds.com/de/ (Standort Karlsruhe), das er m Frühjahr und Sommer 2020 im Rahmen seines Masterstudiums Technomathematik absolviert hat. Bei Dassault Systèmes in Karlsruhe wird schon seit einigen Jahrzehnten Strukturoptimierung betrieben. Wir haben dort auch schon einige Podcastfolgen zu den mathematischen Hintergründen und den aktuellen Weiterentwicklungen aufgenommen (s.u.). Für die numerische Lösung der betrachteten partiellen Differentialgleichungen werden Finite Elemente Verfahren https://de.wikipedia.org/wiki/Finite-Elemente-Methode eingesetzt. Grundlage einer jeden Strukturoptimierung ist ein mathematisches Optimierungsproblem unter Nebenbedingungen. Dazu werden eine Zielgröße und mehrere Nebenbedingungen definiert. Die Zielgröße ist dabei abhängig von zu bestimmenden Variablen, die als Unbekannte oder Optimierungsparameter bezeichnet werden. Die Nebenbedingungen sind Bedingungen an die Variablen, die erfüllt sein müssen, damit die Löung ”zulässig“ ist. Das Ziel der Optimierung ist nun die Minimierung der Zielgröße unter Einhaltung der Nebenbedingungen. Um konkrete Probleme zu lösen, gibt es eine Bandbreite verschiedener Löungsmöglichkeiten, die jeweils auf die Aufgabenstellung zugeschnitten werden. Alle Löser bzw. Minimierungsprobleme haben jedoch gemein, dass sowohl die Konvexität der Zielfunktion https://de.wikipedia.org/wiki/Konvexe_und_konkave_Funktionen als auch die Konvexität des Designgebiets https://de.wikipedia.org/wiki/Konvexe_Menge von fundamentaler Bedeutung für die Lösbarkeit des Problems sind. Strukturoptimierung verändert die Form eines Bauteils oder einer Baugruppe so, dass weniger Material nötig ist, aber vorgegebene Festigkeitsanforderungen (z.B. Spannungen, denen das Teil typischerweise ausgesetzt ist) erfüllt sind. Dabei darf sich die Materialverteilung frei in approximativen Schritten verändern und ist nicht durch eine Vorplanung der prinzipiell einzuhaltenden äußeren Form begrenzt. Dies führt z.B. zur Entstehung von Löchern in der Form des Bauteils, was die Topologie auch im mathematischen Sinne verändert. Das ist kompliziert und einfach zugleich - je nachdem, unter welchem Blickwinkel man es betrachtet. Die Einfachheit ergibt sich aus der Tatsache, dass keine Zellen aus dem numerischen Netz der Numerik entfernt werden. Man setzt einfach eine Variable, die angibt, ob dort Material vorhanden ist oder nicht. Anstatt dies jedoch mit binären Werten zu tun (d.h. Material "an" oder "aus"), ändert man die Materialdichte der Zelle kontinuierlich zwischen [0, 1]. Dabei steht 0 für kein Material und 1 für die volle Materialmenge. Um numerische Probleme zu vermeiden wird statt 0 eine kleine Zahl verwendet. Da diese Modellierung im Allgemeinen zu physikalisch nicht interpretierbaren Ergebnissen führt, bei denen die Zellen weder leer sind noch die volle Menge an Material enthalten, müssen wir sicherstellen, dass der Optimierer dazu neigt, Ergebnisse zu finden, bei denen die Anzahl der Zellen mit mittlerer Dichte minimal ist. Dazu bestrafen wir solche Konstruktionen. Diese Verfahren heißen Solid Isotropic Material with Penalization Method - kurz SIMP-Methode. Strukturoptimierungsaufgaben enthalten in der Regel eine sehr große Anzahl von Designvariablen, in der Praxis sind es nicht selten mehrere Millionen von Variablen, die die Zielfunktion beeinflussen. Demgegenüber ist die Zahl der Nebenbedingungen viel kleiner - oft gibt es sogar nur ein paar wenige. Da Strukturoptimierungsprobleme im Allgemeinem keine konvexen Promleme sind und oft auch keine linearen Probleme, ist die Auswertung des Zielfunktionals und der Nebenbedingungen sehr rechenintensiv. Deshalb wurden spezielle Algorithmen entwickelt, die besonders geeignet für die Lösung solcher Probleme sind, weil sie vermeiden können, dass bis zur Konvergenz eine große Anzahl von Funktionsauswertungen stattfinden müssen. Der wahrscheinlich meist verbreitete Algorithmus heißt Method of Moving Asymptotes (MAA) https://de.wikipedia.org/wiki/Method_of_Moving_Asymptotes. Er wird in der Podcastepisode diskutiert. Die Aufgabe von Attila in seiner Zeit des Praktikums war es nämlich, diese Methode zu verallgemeinern, dann zum implementieren und die Implementierung zu testen. Die ursprünglich angewandte MAA-Methode, die von Svanberg vorgeschlagen wurde, verwendet nur einen sehr einfachen Ansatz zur Behandlung der Länge des Intervalls zwischen der unteren und oberen Asymptote. * LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ * PODCASTS __ __

49m

Jun 20, 2021

Gudrun spricht mit Hartwig Anzt https://hartwiganzt.github.io/. Er leitet die Helmholtz-Nachwuchsgruppe Fixed-point methods for numerics at Exascale (FiNE) https://www.scc.kit.edu/en/aboutus/jrg-fine.php am SCC. Seine Forschung beschäftigt sich mit numerischer linearer Algebra in modernen Hochleistungsrechnersystemen. Angesichts des explosionsartigen Anstiegs der Hardware-Parallelität erfordert die effiziente Ausführung von Anwendungen auf solchen Systemen eine völlige Neugestaltung der zugrunde liegenden numerischen Methoden. Dieses neue Paradigma muss Implementierungen umfassen, die sich auf die Parallelität auf Knotenebene, ein reduziertes globales Kommunikationsvolumen und abgeschwächte Synchronisationsanforderungen konzentrieren. Hartwig ist Teil des PEEKS https://icl.utk.edu/peeks/ und xSDK https://xsdk.info/-Projekts und leitet die Multiprecision-Initiative im US Exascale Computing Project (ECP) https://www.exascaleproject.org/. Das Ziel dieser Initiative besteht darin, die Nutzung verschiedener arithmetischer Präzisionen in numerische Algorithmen zu erforschen, wodurch viele Algorithmen beschleunigt werden können, ohne dabei Genauigkeit einzubüßen. Hartwigs Forschungsschwerpunkt liegt auf der Entwicklung und Optimierung numerischer Methoden https://de.wikipedia.org/wiki/Numerische_Mathematik für effizientes Hochleistungsrechnen. Insbesondere interessiert er sich für lineare Algebra https://de.wikipedia.org/wiki/Lineare_Algebra für dünn besetzte Matrizen https://de.wikipedia.org/wiki/Dünnbesetzte_Matrix, iterative und asynchrone Methoden, Krylov-Löser https://de.wikipedia.org/wiki/Krylow-Unterraum-Verfahren und Vorkonditionierung https://de.wikipedia.org/wiki/Vorkonditionierung. Die zugrundeliegende Idee besteht darin, numerische Probleme als Fixpunktprobleme https://de.wikipedia.org/wiki/Fixpunktiteration umzuformulieren, um höhere Parallelisierungsgrade zu ermöglichen. Die Implementierung der Fixpunktmethoden macht typischerweise starken Gebrauch von (datenparallelen) Batch-Routinen und weist schwache Synchronisationsanforderungen auf. Die Algorithmenforschung wird ergänzt durch Bemühungen, die auf eine nachhaltige Software-Entwicklung in einem akademischen Umfeld und einen gesunden Software-Lebenszyklus https://de.wikipedia.org/wiki/Software-Lebenszyklus abzielen. Ein Ergebnis dieser Bemühungen ist Ginkgo https://github.com/ginkgo-project, eine Open Source Softwarebibliothek für numerische lineare Algebra mit dem Fokus auf Löser für dünn besetzte Systeme, die Hartwig ins Leben gerufen hat. Bei dem Stichwort Software-Nachhaltigkeit könnte man an das Vorhandensein eines Continuous Integration (CI)-Frameworks https://de.wikipedia.org/wiki/Kontinuierliche_Integration denken, also das Vorhandensein eines Test-Frameworks, das aus Unit-Tests https://de.wikipedia.org/wiki/Modultest, Integrationstests und End-to-End-Tests besteht (inkl. das Vorhandensein einer Software-Dokumentation). Wenn man jedoch fragt, was der übliche Todesstoß für ein wissenschaftliches Softwareprodukt ist, ist es oft die fehlende Plattform- und Leistungsportabilität. Vor diesem Hintergrund haben Hartwig und seine Gruppe wir Ginkgo-Bibliothek mit dem primären Fokus auf Plattform-Portabilität und der Fähigkeit, nicht nur auf neue Hardware-Architekturen zu portieren, sondern auch eine gute Performance zu erreichen, entwickelt. Die grundlegende Idee beim Design der Ginkgo-Bibliothek ist eine radikale Trennung der Algorithmen von den hardwarespezifischen Dingen. Daneben sprechen Gudrun und Hartwig über die Nutzung von Kalkülen mit geringer Genauigkeit für letztendlich präzise Algorithmen. Die Hardware-Anbieter haben nämlich damit begonnen, spezielle Funktionseinheiten mit geringer Genauigkeit zu entwickeln, um der Nachfrage z.B. der Machine-Learning-Community und deren Bedarf an hoher Rechenleistung in Formaten mit geringer Genauigkeit zu entsprechen. Hartwig konzentriert sich darauf, wie dann Mixed- und Multiprecision-Technologie helfen kann, die Leistung dieser Methoden zu verbessern und findet Anwendungen, die die traditionellen Methoden mit fester Genauigkeit deutlich übertreffen. * LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ * PODCASTS __ __

54m

May 27, 2021

Diese Folge entstand im Rahmen eines Projekts zur Modellbildungsvorlesung von Gudrun. Es ist eine Arbeit von Yannik Brenner, Bastian Hasenclever und Urs Malottke, die das Ziel haben, in einigen Jahren Mathematik und Physik am Gymnasium zu unterrichten. Außerdem macht Yannik selbst Musik und hat sich deshalb ganz praktisch mit Schwingungen an der Gitarre beschäftigt. Die drei hatten die Idee, dass man das Thema Schwingunge interessant für die Schule aufbereiten kann, wenn es dazu auch Hörbeispiele gibt. Deshalb haben Sie sich an einen Tisch gesetzt, das Gespräch und die Hörbeispiele aufgenommen und schließlich den Text dazu aufgeschrieben. Der harmonische Oszillator spielt eine wichtige Rolle zur Modellierung verschiedenster physikalischer Sachverhalte. Daher bietet es sich an, ihn schon in der Schule zu thematisieren, wo er auch in der Oberstufe im Bildungsplan zu finden ist. Während im Podcast der Versuch unternommen wurde, ein Grundverständnis für das Thema ohne formale Zusammenhänge zu entwickeln, sollen hier zusätzlich die mathematischen Hintergründe gemeinsam mit einigen Abbildungen ergänzt werden. Die didaktischen Aspekte, die in der Episode zur Sprache kommen, spielen im folgenden Text jedoch nur eine untergeordnete Rolle. * GRUNDLEGENDES Ein Oszillator ist ein System, das um einen bestimmten Punkt, in der Regel Ruhepunkt oder auch die Ruhelage genannt, schwingen kann. Befindet sich das System in Ruhe in dieser Ruhelage, passiert ohne die Einwirkung äußerer Kräfte nichts; wird das System von diesem Punkt ausgelenkt, wird es durch eine rückstellende Kraft wieder Richtung Ruhepunkt beschleunigt. Der Zusatz "harmonisch" bedeutet, dass die Rückstellkraft linear von der Auslenkung zum Ruhepunkt abhängt, also proportional zur Auslenkung zunimmt. Der Graph der Bewegungsfunktion ist eine Sinus- oder Cosinus-Kurve. Die einfachsten und wohl auch bekanntesten Beispiele eines Oszillators im Bereich der Mechanik sind das Faden- und das Federpendel. Beim Fadenpendel ist der niedrigste Punkt die Ruhelage und die Rückstellkraft resultiert aus der Gravitationskraft. Beim Federpendel stellt die Federkraft die rückstellende Kraft dar. * EIGENSCHAFTEN EINES HARMONISCHEN OSZILLATORS Ein schwingfähiges System besitzt verschiedene Eigenschaften, mit deren Hilfe das gesamte System beschrieben werden kann. Um den harmonischen Oszillator zu verstehen, kann man sich zuerst die Bewegungsgleichung ansehen, also die Gleichung, die die aktuelle Lage des Systems beschreibt. Ausgangspunkt ist die Rückstellkraft, die im mechanischen Fall linear von der Auslenkung zur Ruhelage, also dem aktuellen Ort, abhängt (auf nicht-mechanische Einsatzgebiete wird später eingegangen). Die Rückstellkraft img kann mit einer Variablen img , die von verschiedenen Merkmalen des Systems abhängt, gemeinsam mit dem Ort also als img dargestellt werden. Die Kraft kann auch als Beschleunigung img , also der zweifachen Ableitung des Ortes, mal der Masse img ausgedrückt werden, wodurch die Formel auch folgendermaßen aussehen kann: img Diese Art von Formeln, in der eine Größe gemeinsam mit einer ihrer Ableitungen auftritt, wird Differentialgleichung genannt. Das Erarbeiten einer Lösung ist leichter, wenn durch img die Gleichung vereinfacht wird. img wird die Eigenfrequenz des Systems genannt und gibt außerdem an, wie viele Schwingungen das System in einer bestimmten Zeit, oftmals einer Sekunde, macht, wenn keine anderen Kräfte vorliegen. Somit ergibt sich img Die Lösung der Funktion für den Ort img muss eine Funktion sein, die nach zweimaligem Ableiten bis auf einen Vorfaktor und das Vorzeichen wieder die Ursprungsfunktion ist. Deshalb sind Sinus- und Cosinus-Funktionen, oder die äquivalente Darstellung durch die e-Funktion (siehe Eulersche Formel https://de.wikipedia.org/wiki/Eulersche_Formel), Lösungen. Werden nun img gewählt, wobei img und img die Amplituden, also maximalen Auslenkungen der Schwingungen darstellen, kann mit den Ableitungsregeln überprüft werden, dass dies Lösungen für die Bewegungsgleichung sind. Als Summe zweier Lösungen ist auch img Eine Lösung, die die allgemeine Lösung genannt wird. Die beiden Amplituden der einzelnen Sinus-/Kosinus-Funktion müssen dabei aus Anfangsbedingungen bestimmt werden. Man sieht, dass img die Amplitude der beobachtbaren Schwingung sein muss, also der maximalen Auslenkung, die beim Zeitpunkt img vorliegt, da die Gesamtschwingung zum Zeitpunkt img diese Auslenkung annehmen muss und zu diesem Zeitpunkt der Sinus verschwindet: img Die Amplitude der Sinus-Funktion bestimmt sich nach img und spielt daher dann eine Rolle, wenn zum Zeitpunkt img bereits eine Geschwindigkeit vorliegt, das System also nicht aus der Ruhe losgelassen, sondern angestoßen wird. Zu besprechen ist allerdings noch, wie die Gleichung bei einem anderen Pendel als dem Federpendel aussieht. Das Prinzip des Oszillators bleibt gleich und somit natürlich auch die Mathematik, die ihn beschreibt. Allerdings setzt sich img bei anderen Pendeln anders zusammen, da bei ihnen andere Rückstellkräfte und andere Systemeigenschaften eine Rolle spielen und nicht die Federkonstante und Masse wie beim Federpendel. So gilt beim Fadenpendel img wobei img die klassische Gravitationskonstante ist, die beim Fadenpendel eine große Rolle für die Rückstellkraft einnimmt, und img die Fadenlänge darstellt. Werden Oszillatoren außerhalb der Mechanik betrachtet, beispielsweise der elektrische Schwingkreis https://de.wikipedia.org/wiki/Schwingkreis, ergibt sich img aus den Eigenschaften, die dieses System beschreiben. Beim elektrischen Schwingkreis z.B. aus der Induktivität img der Spule und der Kapazität img des Kondensators: img Um die Sinus-förmige Schwingung eines Oszillators zu beschreiben, werden noch weitere Begriffe verwendet, die jedoch aus den bisher vorgestellten Eigenschaften bestimmt werden können. So wird unter der Schwingungs- oder Periodendauer img die Zeit verstanden, die das System für eine vollständige Schwingung benötigt. Da sie als Informationen die Anzahl an Schwingungen und eine Zeit enthält, muss sie eng mit der Eigenfrequenz zusammenhängen: img img https://www.leifiphysik.de/sites/default/files/images/9054e0d04b5aff3a1c0455ff209ab02c/992Grundbegriffe%20zu%20Periodischen%20Bewegungen%20und%20Schwingungen_0.svg Überblick über die wichtigsten Begriffe zur Beschreibung einer Schwingung (Quelle: leifiphysik.de http://leifiphysik.de) * UNGEDÄMPFTER HARMONISCHER OSZILLATOR Immer dann, wenn ein schwingfähiges System mit der obigen Gleichung beschrieben werden kann, handelt es sich um einen ungedämpften harmonischen Oszillator. Denn an der Gleichung wird klar, dass die Amplitude, also die maximale Auslenkung, auch bei der 20ten, 100ten, 10.000ten Schwingung wieder erreicht wird. Da sich die Systemeigenschaften ohne äußere Einflüsse ebenfalls nicht ändern, ändert sich das Verhalten dieses Oszillators nie und er schwingt stets gleich um die Ruhelage. Nach der mathematischen Herleitung ist schon fast alles zum ungedämpften harmonischen Oszillator gesagt, denn: Reale Beispiele und Anwendungen gibt es nicht! In der Realität gibt es immer einen Widerstand, der den Oszillator ausbremst und die Auslenkung langsam kleiner werden lässt. Aus diesem Grund ist der ungedämpfte Oszillator nur zum Kennenlernen und Verstehen des Verhaltens sowie als Näherungslösung geeignet. * GEDÄMPFTER HARMONISCHER OSZILLATOR Beim gedämpften harmonischen Oszillator existiert eine bremsende Kraft. Das ändert die mathematische Beschreibung in der Differentialgleichung. Die Bewegungsgleichung des Federpendels (und äquivalent die Gleichungen anderer Oszillatoren) wird um einen Term ergänzt, der im einfachen Fall der Reibung in der Luft, also einem Reibungskoeffizienten img und proportional zur Geschwindigkeit ist: img Oft wird img zu img zusammengefasst, um das rechnen zu vereinfachen. Die zu lösende Differentialgleichung wird auf die gleiche Art gelöst, wird aber natürlich komplizierter. Als Lösungsansätze empfehlen sich wieder Sinus-, Cosinus- oder e-Funktion. Mit dem Ansatz img ergeben sich Lösungen, wenn img die folgende Gleichung erfüllt: img Je nachdem, wie das Verhältnis von Dämpfung und Eigenfrequenz sind, werden verschiedene Fälle unterschieden: * SCHWACH GEDÄMPFTER FALL Der schwach gedämpfte Fall tritt auf, wenn img gilt. Somit ist die Zahl unter der Wurzel bei der Berechnung von img negativ und die Wurzel selbst imaginär. Mit der verkürzten Schreibweise img ergibt sich die allgemeine Lösung zu img was im Vergleich mit der ungedämpften Schwingung eine Schwingung mit kleinerer Frequenz (da img ) und einer mit der Zeit exponentiell abnehmenden Amplitude darstellt. Eine andere Darstellungsweise ist folgende: img Hier ist die exponentielle Abnahme der Amplitude img besser ersichtlich, allerdings ist dazu das Verständnis des Zusammenfassens zweier auftretender periodischer Funktionen mittels Phasenverschiebung https://de.wikipedia.org/wiki/Phasenverschiebung img nötig. Die Schwingung schwingt in diesem Fall weiterhin um die Ruhelage, allerdings wird, wie bereits gesagt, die maximale Auslenkung mit jeder Schwingung geringer. img https://commons.wikimedia.org/wiki/File:Schwingung_ged%C3%A4mpft.svg#/media/Datei:Schwingung_gedämpft.svg Die Einhüllende zu einer gedämpften Schwingung (Quelle: Wikipedia/Harmonischer-Oszillator https://de.wikipedia.org/wiki/Harmonischer_Oszillator) * APERIODISCHER GRENZFALL In Anwendungen ist es oft gewollt, eine Schwingung schnellstmöglich zu stoppen und zur Ruhelage zurückzukehren. Wenn eine Dämpfung keine komplette Fixierung in einem Zustand beinhaltet, ist eine überstarke Dämpfung dabei aber nicht zielführend, wie intuitiv oft angenommen wird. Um die Schwingung schnellstmöglich zu stoppen, ist die Bedingung img nötig. Somit verschwindet in der Berechnung von img die Wurzel und es bleibt nur eine Lösung übrig, was für die Schwingung zu img führt, wobei img und img aus den Anfangsbedingungen, also Auslenkung und Startgeschwindigkeit, bestimmt werden. Beim aperiodischen Grenzfall, manchmal auch mit kritischer Dämpfung bezeichnet, findet keine Schwingung mehr statt. Je nach Anfangsbedingungen kann die Ruhelage einmal durchlaufen werden, spätestens dann wird sich dieser allerdings exponentiell angenährt. img https://commons.wikimedia.org/wiki/File:Aperiodischer_Grenzfall.png#/media/Datei:Aperiodischer_Grenzfall.png Darstellung des aperiodischen Grenzfalls mit unterschiedlichen Startgeschwindigkeiten (Quelle: https://de.wikipedia.org/wiki/Aperiodischer_Grenzfall) * STARKE DÄMPFUNG Zwar führt eine starke Dämpfung auch dazu, dass keine Schwingung stattfindet, allerdings braucht das System lange, um wieder in die Ruhelage zurückzukehren. Deshalb wird dieser Fall auch als Kriechfall bezeichnet. Mathematisch wird er mit der Bedingung img beschrieben, was zu zwei reellen, negativen Ergebnissen für img führt. Die Bewegungsgleichung ergibt damit vereinfacht img wobei img und img wieder aus den Anfangsbedingungen bestimmt werden. Vergleich des Kriechfalls mit dem aperiodischen Grenzfall img Um zu zeigen, dass die vorgestellten Fälle alle von Nutzen sind, werden nun einige Anwendungsbeispiele vorgestellt. So ist der Fall der schwachen Dämpfung für Saiteninstrumente wichtig, da die einzelnen Saiten sich nicht sofort wieder in die Ruhelage begeben dürfen, sondern schwingen müssen, um überhaupt einen Ton erzeugen zu können. Der aperiodische Grenzfall ist beispielsweise für Autofahrer sehr wichtig, da die Stoßdämpfer nach diesem Prinzip funktionieren. Das hat den einfachen Grund, dass das Auto nach der Beanspruchung der Stoßdämpfer schnell wieder in die ideale Straßenlage kommen soll. Würde eine schwache Dämpfung verwendet werden, so würde das Auto noch für längere Zeit auf und ab wippen und die Fahrt eher einer Bootstour ähneln, was wenig komfortabel ist. Bei starker Dämpfung könnte es vorkommen, dass die nächste Beanspruchung nicht ausreichend abgefedert werden kann, da die Feder noch zu stark eingefedert ist. Aber auch die starke Dämpfung hat ihre Anwendungsgebiete. So sind beispielsweise viele Türen in öffentlichen Gebäuden stark gedämpft. Das sorgt für ein langsames und leises Schließen der Türen und verhindert, dass die Tür einer unaufmerksamen Person mit zu viel Geschwindigkeit entgegenfällt und diese eventuell verletzt. * GETRIEBENER OSZILLATOR Bisher wurde der Oszillator ohne äußere Kräfte betrachtet. Liegt solch eine Kraft vor, muss diese in die Bewegungsgleichung integriert werden: img Interessant ist dieser Fall besonders dann, wenn es sich bei der Kraft um eine periodische Kraft handelt, also img . Dieser Fall ist sehr gut mit einem schaukelndem Kind zu vergleichen, welches immer zum gleichen Zeitpunkt mit der gleichen Kraft angeschubst wird. Durch diese von außen aufgebrachte Kraft wird aus der homogenen eine inhomogene Differentialgleichung. Um diese zu lösen muss die Lösung der homogenen Differentialgleichung, welche in dem Abschnitt zu dem gedämpften harmonische Oszillator zu finden ist, mit der sogenannten partikulären Lösung addiert werden. img Die partikuläre Lösung lässt sich mit dem Ansatz des Typs der rechten Seite lösen und ergibt sich zu img dabei handelt es sich bei img um eine Phasenverschiebung zwischen der antreibenden Kraft und dem um den Ruhepunkt schwingenden Massepunkt. Von besonderem Interesse ist dabei das Verhalten des gesamten Systems für verschiedene Frequenzen der treibenden Kraft. Dabei werden drei verschiedene Fälle betrachtet. * Niederfrequenter Bereich: img Für den niederfrequenten Bereich gilt, dass die Frequenz der antreibenden Kraft sehr viel kleiner ist als die Eigenfrequenz des Oszillators. Aufgrund dessen ist die Amplitude der anregenden Kraft in etwa so groß wie die Amplitude des Massepunktes. Das Amplitudenverhältnis beträgt also ungefähr 1. Der Phasenunterschied zwischen den beiden Schwingungen ist in etwa 0. * Resonanzfall: img Von Resonanz wird gesprochen, wenn die Frequenz der antreibenden Kraft der Eigenfrequenz des Oszillators gleicht. Infolgedessen erhöht sich die Amplitude des Oszillators gegenüber der Amplitude des Erregers, sodass sich ein Amplitudenverhätnis ergibt, welches größer 1 ist. Die Phasendifferenz beträgt img , wobei der Erreger dem Massepunkt vorauseilt. * Hochfrequenter Bereich: img Sollte die Frequenz der antreibenden Kraft viel größer sein als die Eigenfrequenz des Oszillators so fällt auch die Amplitude des Oszillators wesentlich kleiner aus. Es ergibt sich ein Amplitudenverhätnis, welches gegen 0 geht. Auch in diesem Fall gibt es eine Phasendifferenz img , die Schwingungen laufen also fast gegenphasig ab. Auch diese Eigenschaften der Oszillatoren sind im Alltag von Bedeutung. So ist es für Autos wichtig, dass die Eigenfrequenz einzelner Teilsysteme oder des Gesamtsystems nicht im Bereich der Motorendrehzahl liegen um eine komfortable und sichere Fahrt zu gewährleisten. Insbesondere der Resonanzfall kann gefährliche Auswirkungen haben, da in diesem Fall das System immer weiter aufgeschaukelt wird und die Amplitude des Oszillators sich immer weiter erhöht. Falls das System nicht gedämpft ist, kann die Amplitude bis ins Unedliche steigen, was zur Zerstörung des Systems führt. Eine starke Dämpfung kann die maximale Amplitude zwar begrenzen, aber auch in diesem Fall komm es für den Resonanzfall zu einer starken Belastung des Systems, was in den meisten Fällen vermieden werden sollte. Ein gutes Beispiel für eine Resonanzkatastrophe ist die Tacoma Narrows Bridge https://de.wikipedia.org/wiki/Tacoma-Narrows-Br%C3%BCcke#Die_Br%C3%BCcke_von_1940, welche durch starke Winde in Schwingung versetzt wurde, welche sich dann selbsterregt immer weiter verstärkte, was den Einbruch der Brücke zur Folge hatte. Demgegenüber bleibt aber zu sagen, dass ohne Resonanz auch viele alltägliche Dinge nicht möglich wären, es also auch einen positiven Aspekt gibt. So würde Schaukeln nicht halb so viel Spaß machen, wenn es nicht möglich wäre seine eigene Schwingung zu verstärken und somit immer höher Schaukeln zu können. Ein weiteres typisches Beispiel für den getriebenen harmonischen Oszillator stellt der elektrische Schwingkreis da, der bei der drahtlosen Energieübertragung genutzt wird. Das System wird dabei ständig neu mit Energie aufgeladen, die es dann mittels sogenannter resonant induktiver Kopplung an einen Empfänger weitergeben kann, der so kabellos geladen wird. * WEITERFÜHRENDES Viele weiterführende Beispiele, die sich des Oszillators mit schwacher Dämpfung bedienen, sind in der Akustik respektive Musik zu finden, wie die Schwingung einer (Gitarren-)Seite, die nach einmaligem Anschlag möglichst lange klingen soll. Doch hier handelt es sich nicht um einen einfachen harmonischen Oszillator, sondern um ein komplexeres System. * LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ * PODCASTS __ __

30m

Apr 23, 2021

Im Rahmen der Vorlesung Mathematical Modelling and Simulation haben Jan Dietrich und Alexander Grötz ein Projekt bearbeitet, wo sie Verkehr mit Hilfe der Software VISSIM simulieren. Die Idee kam ihnen durch ein Praktikum Firma ptvgroup http://www.ptvgroup.com/de/willkommen-bei-der-ptv-group/ an der Verkehrsmodellierung, das Jan Dietrich kürzlich dort absovliert hat. Im Gespräch geht es um verschiedene Formen der Modellierung von Verkehrsflüssen und um konkrete Umsetzung des Modells in VISSIM. Der ersten Teil des Podcasts ist dabei der theorietischen Ausgestaltung von Verkehrsmodellen gewidmet. Im Wesentlichen unterschiedet man zwischen zwei Gruppen von Verkehrsmodellen. Während die so genannten Verkehrsflussmodelle, die die zeitliche Veränderung des Verkehrsaufkommens untersuchen, werden Verkehrsnachfragemodelle dazu verwendet, um Aussagen über das Verkehrsaufkommen in einem Jahr oder die Aufteilung dieser Nachfrage auf die verschiedenen Transportmittel zu treffen. Weiter werden diese beiden Gruppen nochmals in drei Kategorien uterteilt; genauer in __ __ Eine letzte Unterscheidungsmöglichkeit zwischen einzelnen (Verkehrs-)Modellen ist der Zufall: Wenn jede Modellvariable in dem Sinn "vorhersehbar", dass die quantitative Ausprägung der einzelnen Variablen für alle betrachteten Zeiten exakt berechenbar sind und über deren Ausprägung keine Unsicherheit herrscht, sprich man von deterministischen Modellen. Oft ist es jedoch so, dass man bestimmte Ereignisse oder auch Handlungen der einzelnen Verkehrsteilnehmer nicht exakt vorhersehen kann. Dadurch erhält man aber gewisse Unsicherheiten bei der Berechnung zukünftiger Zustände, weil man die genaue Ausprägung der zufälligen Größen erst ex post kennt. Man wird im Allgemeinen also nie den exakten Zustand eines Modells mit solchen zufälligen Einflussgrößen bestimmen können. Solche Modelle, die Zufallsvariablen beinhalten, nennt man stochastisch. Im zweiten Teil des Podcasts, geht es um die praktische Umsetzung von Verkehrsmodellen mit Hilfe der Software PTV VISSIM. In VISSIM werden zahlreiche Aspekte des Straßenverkehrs sehr realitätsnah und graphisch ansprechend abgebildet. Neben der reinen Simulation der Bewegung von Fahrzeugen wird dabei auch auf viele Details, die das Verhalten der Fahrzeuge in der Realität beeinßussen, Rücksicht genommen. Unter anderem werden verschiedene Fahrzeugklassen und deren unterschiedliches Verhalten beim Bremsvorgang berücksichtigt, aber auch Dinge wie Vorfahrtsregelungen und Spurwechsel können modelliert werden. Mit der Erweiterung PTV Viswalk kann sogar auf das Verhalten einzelner Fußgänger Rücksicht genommen werden. Die Modellierung der Bewegung der einzelnen Verkehrsteilnehmer in PTV Vissim basiert dabei grundlegend auf dem Fahrzeugfolgemodell von Rainer Wiedemann, einem s.g. mikroskopischen, stochastischen Verkehrsfolgemodell, in welches auch psychologische Aspekte der Verkehrsmodellierung mit einfließen. Um auch den Zuhörern des Podcasts, einen ersten Eindruck von VISSIM vermitteln zu können, hat Jan sich bereit erklärt, die grundlgenden Funktionen von VISSIM in einem kurzen Einführungsvideo https://youtu.be/pASkiCajiYw vorzustellen. Weitere Modellierungsmöglichkeiten mit VISSIM findet man z.B in der zum Podcas gehörenden Ausarbeitung https://studentkit-my.sharepoint.com/:b:/g/personal/uhejr_student_kit_edu/ETIDPemi5_1Mv0VciBmF2X0BVQZw5e4YX6plwsyGqD7OKg?e=q6u9iu, die neben der Einführung in VISSIM auch einen Überblick über das Verkhsmodellierung im Allgemeinen gibt. Wie man im Einführungsvideo gut sehen kann, muss man für eine möglichst realitätsnahe Modellierung des Straßenverkehrs einige Parameter einstellen. Sinnvolle Kenngrößen für in die Simulation eingehenden Daten (wie z.B. das Verkehrsaufkommen in den einzelnen Fahrbahnen, Beschleunigung und Bremsstärke für einzelne Fahrzeugklassen, die Schaltung der Ampeln, etc.) müssen vor der Eingabe in Vissim zuerst aber noch ermittelt werden. Oft, wie beispielsweise beim erwarteten Verkehrsaufkommen, erfordert dies wiederum eigene Modelle. Einen guten Überblick über das Thema Verkehrsplanung, insbesondere im Zusammenhang mit dem Thema der Verkehrsnachfrage, bietet beispielsweise das Paper von Firedrich https://www.isv.uni-stuttgart.de/vuv/publikationen/downloads/2011_Friedrich_Nachfragemodelle_Heureka2011_mit_Deckblatt.pdf. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

39m

Oct 02, 2020

Im Mai 2020 sprach Gudrun mit Verena Knoblauch https://twitter.com/VerenaKnoblauch. Sie ist Lehrerin und Medienpädagogin. Sie arbeitet in einer Nürnberger Grundschule und hat dort Tabletklassen im dritten und vierten Schuljahr unterrichtet. Gudrun und Verena sind sich auf Twitter begegnet. Dort gibt es eine sehr aktive und bunte Gruppe von Lehrpersonen, die sich unter dem Hashtag #twitterlehrerzimmer https://twitter.com/search?q=%23twitterlehrerzimmer austauschen. Es gibt auch schon ein anderes Podcastgespräch "aus dem twitterlehrerzimmer" mit Jan-Martin Klinge zu den von ihm verwendeten Lerntheken. Unter dem Eindruck der Corona-Einschränkungen wollte Gudrun gern aus erster Hand erfahren, wie Verena den Unterricht aus der Ferne für die jüngsten Schülerinnen und Schüler gestaltet und erlebt. Verena berichtete, dass es für die Kleinen ohne Präsenzunterricht schwierig ist, da für sie neben den Inhalten des Unterrichts der Kontakt zu Lehrern und Mitschülern mindestens ebenso wichtig ist. Die Gemeinschaft in der Klasse lässt sich aber im Fernunterricht nicht gut herstellen. Verena steht im Zwiespalt wie alle Lehrpersonen: Verteilt man Arbeitsblätter, dann ist den Kindern und deren Eltern recht klar, was genau erledigt werden soll. Aber das ist nach kurzer Zeit schon langweilig. Auch für die Lehrpersonen. Deshalb werden Kolleginnnen und Kollegen auch sehr kreativ bei der Erstellung von freieren Aufgaben. Leider sind dann aber oft die Eltern überfordert und ohne Eltern geht Fernunterricht in der Grundschule nicht. In ihrer Tätigkeit als Grundschullehrerin - auch ohne Corona - gibt es eigentlich keinen Alltag und keine Routine. Verena sieht eine wichtige Rolle darin, zu unterichten wie man sich bei Fragen zu helfen weiß, z.B. mit der Kindersuchmaschine fragFinn http://www.fragfinn.de/. Sie stellt sich nicht als allwissende Lehrperson mit Wissenshoheit vor die Klasse, denn es ist auch für die Kinder wichtig zu lernen: Keiner weiß alles. Und es ist eine wichtige Kompetenz, nicht nur die Eltern oder andere Erwachsene fragen zu müssen, sondern selbst zu suchen und zu finden und mit den Ergebnissen souverän umgehen zu können. Was ist vernünftig, was stimmt, was ist ganz bestimmt Quatsch? Seit einigen Jahren schon setzt Verena in ihren 3. und 4. Klassen auf die Unterstützung durch Tablets für den Unterricht. Die Anregung hierzu kam von außen in Form einer Spende von zwei Klassensätzen Tablets für die Grundschule. Nachdem sie spontan zugesagt hatte, dass sie diese gern für ihren Unterricht einsetzen möchte, musste sie sich zunächst einmal damit beschäftigen, wie man das verwaltet, versichert, aufbewahrt und pflegt. Und mehr darüber lernen, was man nun damit anfangen kann. Hierzu hilft der Austausch mit Kolleginnen aus nah und fern. Verena hat sich aber sogar entschieden dafür noch Medienpädagogik zu studieren. Als erstes fallen einem im Zusammenhang mit Tablets im Unterricht natürlich Übungsapps ein, die es für viele Fächer gibt, wo die Kinder auf sie zugeschnittene Aufgaben finden und gleich Rückmeldung bekommen, was sie richtig gemacht haben. Verena stellte jedoch fest, dass man mit Tablets viel viel mehr machen kann. In Film und Ton und mit Bildern können die Kinder ihre Ideen ausdrücken und sogar erklären, warum sie Sachen so machen und damit zeigen, was sie wie verstanden haben. In einem Projekt haben die Kinder Informationen zu bestimmten Ländern als Reportagen präsentiert, die vor einem Greenscreen aufgezeichnet wurden. Dann konnte ein Bild des Landes als Hintergrund eingefügt werden und schon wirkte es wie ein Bericht vor Ort. Oder eine Lesekiste wird gebastelt, wo eine Szene aus einem Buch nachgebaut wird. "Darin" kann man dann über das Buch berichten, nachdem ein Foto, das in der Kiste aufgenommen wird hinter den Filmbericht gelegt wird. Von dort ist es nur ein kleiner Schritt, zu verstehen wie leicht es ist, nur den Anschein von Wahrheit zu erwecken. Verena ist dann noch etwas weiter gegangen und hat die Schülerinnen und Schüler Fake News produzieren lassen, die professionell aussehen. Wenn man als Drittklässler mit drei Clicks Bilder fälschen kann, dann schaut man sich anderswo Informationen automatisch viel kritischer an. Inzwischen arbeitet Verena in der Fortbildung für Kollegen. Zur Zeit auschließlich in der Form von Webinaren. So kann sie Ihre Erfahrung mit den Möglichkeiten der Tablets im Unterricht recht niederschwellig an Kolleginnen und Kollegen weiter geben. Außerdem ist es interessant, auch Lehrerin für Erwachsene zu sein. Und es hilft ihr davon weg zu kommen als Einzelkämpferin zu arbeiten, wie es in der Schulzeit und im Examen an der Uni gelernt wird. Statt dessen ist es für sie und alle Lehrpersonen ein großer Gewinn, sich zu öffnen und z.B. bei Twitter oder in Fortbildungen neues lernen und von den Ideen der anderen zu profitieren. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

38m

Aug 20, 2020

Gudrun spricht mit Petra Schwer https://www.geometry.ovgu.de/schwer.html und Thomas Kahle https://thomas-kahle.de/. Alle drei sind während des Gesprächs jeweils in ihrem Wohnzimmer und treffen sich auf einer Videoplattform. Deshalb ist es etwas schwieriger, stets nur nacheinander zu sprechen. Petra und Thomas sind an der Otto von Guericke Universität https://www.uni-magdeburg.de/ in Magdeburg Professorin bzw. Professor am Institut für Algebra und Geometrie. Der Anlass des Gespräches ist, dass die beiden kürzlich einen Mathepodcast gestartet haben, nämlich Pi ist genau drei https://pi-ist-genau-3.de/. Zur Zeit des Gespräches, im April 2020, waren dort die ersten drei Episoden veröffentlicht mit den Themen __ __ Im Podcast Pi ist genau drei ist jeweils eine der beiden Personen auf das Thema vorbereitet, die andere wird "überrascht". Als Publikum kann man auf diese Art und Weise die beiden beim Denken und Ideen entwickeln beobachten und sich zum mitdenken anregen lassen. Im Gespräch von Gudrun, Thomas und Petra geht es darum, wie man Mathematik im Podcastformat darstellen kann. Welche Erfahrungen und Wünsche wurden von ihnen gemacht? Inwieweit gehört Mut dazu, sich relativ ungeschützt beim Diskutieren und Ideen Entwickeln zu zeigen und welche Vorteile hat es, diesen Mut aufzubringen? Davon ausgehend reden Sie auch darüber, wie sich Aspekte des Nachfragens und des offenen Denk-Raumes auch in der Lehre realisieren lassen sollten. Weil sie selbst durch andere Podcasts inspiriert worden sind, es selbst zu versuchen, empfehlen sie auch ihre Lieblingspodcasts. WEITERE INFORMATIONEN Der Titel des Podcasts spielt auf eine Szene der Serie Die Simpsons https://de.wikipedia.org/wiki/Die_Simpsons an. In dieser Episode (S12E16 „Bye Bye Nerdy“, dt: „Lisa knackt den Rowdy-Code“) verschafft sich Professor Frink durch die schockierende Aussage „Pi ist genau drei!“ die Aufmerksamkeit seiner Kollegen https://www.youtube.com/watch?v=L1eegVTwDS0. PODCASTS __ __ Podcast-Empfehlungen von Thomas, Gudrun und Petra: __ __ Thomas hat den Modellansatz kennengelernt über die Folge: __ __

1h 11m

May 09, 2020

Gudrun sprach im März 2020 mit Nicole Ludwig https://www.iai.kit.edu/2154_2161.php. Sie ist eine Kollegin am KIT am Campus Nord und gehört dem Institut für Automation und angewandte Informatik https://www.iai.kit.edu/index.php an. Sie war Mitglied des DFG Graduiertenkollegs Energiezustandsdaten Informatikmethoden zur Analyse, Erfassung und Nutzung https://www.energiezustandsdaten.kit.edu/index.php und ist dabei, ihre Promotion abzuschließen. Im Studium wurde sie von den Themen der Ökonometrie https://de.wikipedia.org/wiki/%C3%96konometrie und Statistik https://de.wikipedia.org/wiki/Statistik eingefangen und von der Freude, aus empirischen Daten verlässliche Ergebnisse ableiten zu können. Sie hat schon in ihrer Bachelorarbeit Maschinelles Lernen https://de.wikipedia.org/wiki/Maschinelles_Lernen für Prognosen benutzt. Deshalb war es sehr spannend für sie, diese Kenntnisse und ihre Freude am Thema in das Graduiertenkolleg zu Energiedaten und Informatik einzubringen. Als Gesellschaft müssen wir in naher Zukunft eine Energieproduktion ohne fossile Brennstoffe erreichen. Es ist jedoch nötig, beim Nutzen von erneuerbaren Energien im Vergleich zu konventioneller Energieerzeugung umzulernen, um einerseits für eine stabile Versorgung von Wirtschaft und Haushalten zu sorgen und andererseits dabei alle Lasten der nötigen Veränderungen fair zu verteilen. Es gibt zwei Möglichkeiten, die Energieproduktion zu optimieren. Zum einen können wir den Produktionszeitplan besser auf die Nachfrage abstimmen. Zum anderen können wir das Verbrauchsverhalten ändern, um eine optimale Versorgungsstrategie zu unterstützen. Traditionell kennt man Prognosen für die Energienachfrage in unterschiedlichen Zeithorizonten und macht diese zur Grundlage für Produktionspläne. Mit einer zunehmenden und sich ändernden Menge an Variablen, die das System beeinflussen, sind perfekte Vorhersagen jedoch sehr unrealistisch und wahrscheinlich nicht der richtige Ansatz für die Zukunft. Man muss sich hierzu nur vor Augen halten, dass die Energieernte sowohl bei Windkraft als auch für Solarstrom stark vom Wetter abhängen. Wenn auch die Wettervorhersage schon sehr viel besser geworden ist, so ist es doch noch nicht möglich, auf ihrer Grundlage hinreichend sichere Vorhersagen für die Energieerzeugung machen zu können. Andererseits gibt es heute auch bessere Möglichkeiten, die Energieabnahme zumindest im Prinzip von außen zu steuern. Das was früher als Nachtstrom die Abnahme von Stromspitzen mit niedrigen Preisen versüßte, kann heute ganz regional und sich täglich anpassend nicht nur in Betrieben sondern sogar im Haushalt steuern, wann beispielsweise die Waschmaschine läuft oder ein Warmwasserspeicher lädt. Bald kann auch die Flotte an E-Fahrzeugen mit ihren Akkumulatoren Energie zum passenden Zeitpunkt abnehmen und auch in Spitzenzeiten wieder abgeben. Die Gesetzgebung ist hier noch nicht so weit wie die technischen Möglichkeiten. Aber man muss sicher auch noch einmal gründlich darüber nachdenken, in welcher Art und Weise man Personen dazu zwingen will, Daten dafür zur Verfügung zu stellen und wie man sie anschließend vor dem Missbrauch dieses Wissens durch Unbefugte schützen kann. Schon heute ist die Energieversorgung viel verwundbarer durch Angriffe von Hackern https://de.wikipedia.org/wiki/Hackerangriff_auf_die_ukrainische_Stromversorgung_2015 als wir uns eingestehen wollen. Prinzipiell liegen aber - schon allein in Bezug auf Wetterdaten - aber auch in feingranularem Wissen über Energieverbrauch - sehr viele Daten vor, die man nutzen kann, um neuartige Prognosen zu erarbeiten. Man geht also über von rein Physik-basierten Modellen und Expertenwissen über zu neuronalen Netzen und Datamining. Diese arbeiten natürlich nicht sinnvoll ohne den Expertenblick, denn welche Fragen die vorliegenden Daten sinnvoll und recht sicher beantworten können, ist naiv geplant sicher nicht möglich. Nicole gefällt es gut, an der Schnittstelle sehr unterschiedlicher Wissensgebiete (Wirtschaft, Physik/Meteorologie, Ingenieurswissenschaft und Informatik) zu forschen. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __ __ __

39m

Mar 26, 2020

Gudrun sprach Mitte März 2020 mit Franziska Blendin https://twitter.com/FranziskaNaja. Das Gespräch fand statt, während beide sich in ihrem jeweiligen Wohnzimmern aufhielten: Gudrun in Karlsruhe und Franziska in Frankfurt (Main). Seit drei Semestern absolviert Franziska ein Online Studium an der Fachhochschule Frankfurt https://www.frankfurt-university.de/ und strebt einen Bachelor in Maschinenbau https://www.frankfurt-university.de/fileadmin/standard/Studium/Studiengaenge/Fb_2/Bachelor-Studiengaenge/Maschinenbau_Online/Bilder/Modultafel_Hompage_MOnline.jpg an. Gudrun wollte gern von ihr erfahren, wieso sie sich für diesen Weg entschieden hat und was ihre Erfahrungen mit dieser besonderen Art des Studiums sind. Franziska hat nicht im Gymnasium Abitur gemacht, sondern ein Fachabitur im Rahmen einer Ausblidung zur Sozialassistentin im Fachbereich Pflege. Während ihrer Tätigkeit als Assistentin einer Rollstuhlfahrerin kam die Idee auf, dass sich Franziska bei dem Rollstuhlhersteller schlau machen könnte, um auch kleine Reparaturen oder Anpassungen an dem Gerät übernehmen zu können. So kam es zu einem Praktikum in dem mittelständischen Unternehmen, das den Rollstuhl herstellt. In der Zeit wuchs ihr die Flex ans Herz und es wurde die Idee geboren, so einen Beruf zu erlernen. Sie hat als Zerspanerin und Schlosserin gearbeitet, wollte allerdings auf jedenfall noch eine Fortbildung machen. Im Prinzip hätten zunächst die Möglichkeiten, einen Meister zu machen oder eine Techniker-Ausbildung neben dem Beruf zu absolvieren nahe gelegen. Aber die Erfahrung zeigte Franziska, dass es als Frau ohnehin nicht so leicht ist, für diese Stellen in die engere Wahl zu kommen und dass diese handwerkstypischen Abschlüsse häufig nicht entsprechend gewürdigt werden. Vom Lernaufwand neben der Erwerbsarbeit sind diese Wege aber ähnlich. So hat sich Franziska für ein online Studium entschieden. Der große Vorteil ist, dass es zeitlich flexibler ist und deshalb leichter mit einer Berufstätigkeit passend gemacht werden kann. Bei 100% Job schafft man aber nicht so viel, wie der ideale Plan bis zum Bachelor vorsieht, sondern eher so 3-4 Fächer (das sind 15-20 Leistungspunkte statt der im Plan avisierten 30 Punkte pro Semester - jeder Leistungspunkt entspricht dabei etwa 30 Zeitstunden Aufwand). Hinzu kommt, dass eigentlich alle, deren Abitur schon eine Weile zurück liegt und die vielleicht ein Schmalspurabi wie Franziska haben, Probleme mit Mathe und anderen Naturwissenschaften haben. Franziska ist z.B. sehr froh, dass sie nun nach drei Semestern endlich Mathe 1 bestanden hat (Mathe 2 fiel ihr dann nicht so schwer). Für jedes Modul sind drei Anwesenheitszeiten pro Semester geplant, die ausnahmsweise auch als Webkonferenz durchgeführt werden, in der die Studierenden Fragen stellen können. Den Stoff muss man sich vorher selbst z.B. mit Hilfe eines Lernprogramms oder dem Skript erarbeiten. Wöchentlich gibt es 60-90 min Vorlesung als Webkonferenz - das ist aber mehr eine Zusammenfassung des Stoffs und reicht nicht, um den Stoff zu verstehen. Außerdem müssen noch zwei Hausarbeiten eingesendet werden, um zur Prüfung zugelassen zu werden. Franziska freut sich darauf, bald Anwendungen der Mathematik im Fach Technische Schwingungen und Regelungstechnik zu sehen. Und auch die Module Technische Mechanik 1,2 und 3 waren schon viel Mathematik, haben aber Spaß gemacht. Sie hat die drei Module sofort bestanden obwohl das als schwieriges Fach gilt. In der Thermodynamik hilft ihr auch die Erfahrung aus der Berufspraxis sehr. Franziskas Vater war Mathelehrer und ist eigentlich im Ruhestand. Allerdings ist er inzwischen als Tutor für Mathe 1 an der Hochschule in Frankfurt tätig und als Team haben er und Franziska nun die Prüfung in Mathe 1 zu den Akten gelegt. Gudrun und Franziska haben sich im November 2017 beim Podäppler Workshop https://sendegate.de/t/podaeppler-podcasts-rhein-main/775 in Frankfurt kennengelernt. Gudrun kannte zu dem Zeitpunkt Tine Nowak https://wissenschaftspodcasts.de/blog/tine-nowak-kulturkapital-ein-bildungspodcast/ aus Frankfurt aus dem Netzwerk der Wissenschaftspodcaster https://wissenschaftspodcasts.de/podcasts/ und Tine hatte Gudrun schon mehrfach nach Frankfurt zum Podcaster Stammtisch eingeladen bis es endlich für den Workshop geklappt hat. Franziska macht mehrere Podcasts und zwar über Fußball, Kinderbücher und Zerspanungsmaschinen. Außerdem malt sie Mathecomics - vor allem in heißen Lernphasen. Und weil das noch nicht genug ist, hat sie eine Fußballfibel über den FSV Frankfurt geschrieben, die gerade erschienen ist. Die wegen der Corona-Quarantäne ausgefallene Lesereise holt sie gerade per Youtube Livestreams nach. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS VON FRANZISKA __ __ PODCASTS ZUM THEMA __ __

1h 2m

Mar 19, 2020

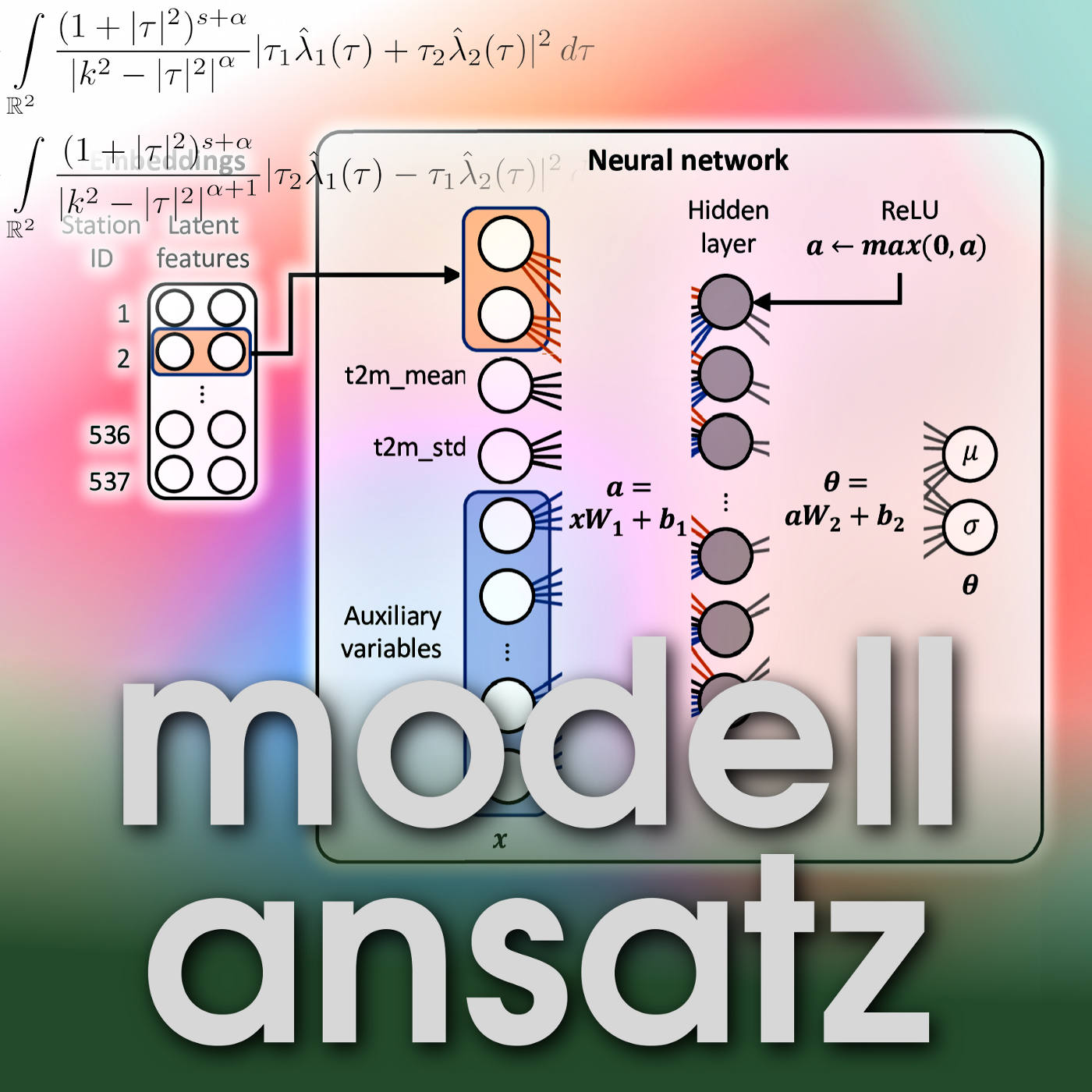
Gudrun spricht mit Sebastian Lerch https://sites.google.com/site/sebastianlerch/ vom Institut für Stochastik http://www.math.kit.edu/stoch/ in der KIT-Fakultät für Mathematik. Vor einiger Zeit - Anfang 2015 - hatten die beiden schon darüber gesprochen, wie extreme Wetterereignisse stochastisch modelliert http://www.modellansatz.de/extremereignisse werden können. Diesmal geht es um eine Lehrveranstaltung, die Sebastian extra konzipiert hat, um für Promovierende aller Fachrichtungen am KIT eine Einführung in Machine Learning zu ermöglichen. Der Rahmen hierfür ist die Graduiertenschule MathSEED http://www.mathsee.kit.edu/mathseed.php, die ein Teil des im Oktober 2018 gegründeten KIT-Zentrums MathSEE http://www.mathsee.kit.edu/ ist. Es gab schon lange (und vielleicht immer) Angebote am KIT, die insbesondere Ingenieure an moderne Mathematik heranführten, weil sie deren Methoden schon in der Masterphase oder spätestens während der Promotion brauchten, aber nicht durch die klassischen Inhalten der Höheren Mathematik abgedeckt werden. All das wird nun gebündelt und ergänzt unter dem Dach von MathSEED. Außerdem funktioniert das nun in beide Richtungen: Mathematiker:innen, werden ebenso zu einführenden Angeboten der anderen beteiligten Fakultäten eingeladen. Das Thema Maschinelles Lernen und Künstliche Intelligenz https://de.wikipedia.org/wiki/Maschinelles_Lernen war ganz oben auf der Wunschliste für neu zu schaffende Angebote. Im Februar 2020 hat Sebastian diese Vorlesung erstmalig konzipiert und gehalten - die Übungen wurden von Eva-Maria Walz betreut. Die Veranstaltung wird im Herbst 2020 wieder angeboten. Es ist nicht ganz einfach, die unterschiedlichen Begriffe, die für Künstliche Intelligenz (kurz: KI) benutzt werden gegeneinander abzutrennen, zumal die Sprechweisen in unterschiedlichen Kontexten unterschiedlich sind. Hinzu tritt, dass mit der Verfügbarkeit großer Datenmengen und der häufigen Nutzung von KI und Big Data gemeinsam auch hier vieles vermischt wird. Sebastian defininiert Maschinelles Lernen als echte Teilmenge von KI und denkt dabei auch daran, dass z.B. symbolisches Rechnen KI ist. Ebenso geben schon lange sogenannte Expertensysteme https://de.wikipedia.org/wiki/Expertensystem Hilfestellung für Entscheidungen. Hier geben Regeln ein Programm vor, das Daten-Input zu einem Output verwandelt. Heute denken wir bei KI eher daran, dass z.B. der Computer lernt wie ein Bild eines Autos aussieht, ohne dass dafür klare Regeln vorgegeben werden. Dies ist eher vergleichbar damit, wie Kinder lernen. Die modernste Variante ist sogenanntes Deep Learning https://de.wikipedia.org/wiki/Deep_Learning auf der Basis von Neuronalen Netzen https://de.wikipedia.org/wiki/K%C3%BCnstliches_neuronales_Netz. Die Abgrenzung zu statistischen Verfahren ist mitunter nicht so klar. Das Neuronale Netz wird dabei eine Black Box, was wissenschaftlich arbeitende Menschen nicht ganz befriedigt. Aber mit ihrer Hilfe werden komplexere Probleme lösbar. Forschung muss versuchen, die Entscheidungen der Black Box nachvollziehbar zu machen und entscheiden, wann die Qualität ausreicht. Dazu muss man sich überlegen: Wie misst man Fehler? In der Bildverarbeitung kann es genügen, z.B. falsch erkannte Autos zu zählen. In der Wettervorhersage lässt sich im Nachhinein feststellen, welche Fehler in der Vorhersage gemacht wurden. Es wird unterschiedliche Fehlertoleranzen geben für Erkennung von Fußgängern für selbst fahrende Autos und für die Genauigkeit von Wettervorhersage. Ein Beispiel in der Übung war die Temperaturvorhersage anhand von vorliegenden Daten. Die Vorhersage beruht ja auf physikalischen Modelle in denen die Entwicklung von Temperatur, Luftdruck und Windgeschwindigkeit durch Gleichungssysteme nachgebildet wird. Aber diese Modelle können nicht fehlerfrei berechnet werden und sind auch recht stark vereinfacht. Diese Fehler werden mit Hilfe von KI analysiert und die Ergebnisse für die Verbesserung der Vorhersage benutzt. Ein populäres Verfahren sind Random Forests oder Entscheidungsbäume. Hier werden komplexe Fragen stufenweise zerlegt und in den Stufen einfache Ja- oder Nein-Fragen beantwortet. Dies wird z.B. angewandt in der Entscheidung ob und wo eine Warnung vor einer Gewitterzelle erfolgen sollte. Sehr bekannt und im praktischen Einsatz erprobt (beispielsweise in der Bildverarbeitung und in der Übersetzung zwischen gebräuchlichen Sprachen) sind Neuronale Netze https://de.wikipedia.org/wiki/Neuronales_Netz. In mehrern Schichten sind hier sogenannte Neuronen angeordnet. Man kann sich diese wie Knoten in einem Netz vorstellen, in dem Daten von Knoten zu Knoten transportiert werden. In den Knoten werden die ankommenden Daten gewichtet aufaddiert und eine vorher festgelegte Aktivierungsfunktion entscheidet, was an die nächsten Knoten oder die nächste Schicht von Neuronen weitergegeben wird. Die einzelnen Rechenoperationen sind hier also ganz elementar, aber das Zusammenwirken ist schwer zu analysieren. Bei vielen Schichten spricht man von Deep Learning. Das ist momentan noch in den Kinderschuhen, aber es kann weit reichende Konsequenzen haben. In jedem Fall sollte man Menschen im Entscheidungsprozess beteiligen. Die konkrete Umsetzung hat Sebastian als Vorlesung und Übung zu gleichen Teilen gewählt. Er hat einen Schwerpunkt auf einen Überblick zu methodischen Aspekten gelegt, die die Teilnehmenden dazu befähigt, später selbst weiter zu lernen. Es ging also unter anderem darum, wie man Trainingsdaten auswählt, wie Qualitätssicherung funktioniert, wie populäre Modelle funktionieren und wie man einschätzt, dass die Anpassung an Daten nicht zu stark erfolgt. In der Übung fand großen Anklang, dass ein Vorhersagewettbewerb der entwickelten Modelle durch Kaggle competions https://www.kaggle.com/competitions online live möglich war. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ ____ __ ____ __ ____ __ ____ __ ____ PODCASTS __ __

41m

Mar 05, 2020

In March 2018 Gudrun had a day available in London when travelling back from the FENICS workshop https://fenicsproject.org/fenics18/ in Oxford. She contacted a few people working in mathematics at the University College London https://en.wikipedia.org/wiki/University_College_London (ULC) and asked for their time in order to talk about their research. In the end she brought back three episodes for the podcast. This is the second of these conversations. Gudrun talks to Marta Betcke http://www0.cs.ucl.ac.uk/people/M.Betcke.html. Marta is associate professor at the UCL Department of Computer Science, member of Centre for Inverse Problems and Centre for Medical Image Computing http://vis.cs.ucl.ac.uk/home/. She has been in London since 2009. Before that she was a postdoc in the Department of Mathematics https://www.maths.manchester.ac.uk/ at the University of Manchester https://www.manchester.ac.uk/ working on novel X-ray CT scanners for airport baggage screening. This was her entrance into Photoacoustic tomography https://en.wikipedia.org/wiki/Photoacoustic_imaging (PAT), the topic Gudrun and Marta talk about at length in the episode. PAT is a way to see inside objects without destroying them. It makes images of body interiors. There the contrast is due to optical absorption, while the information is carried to the surface of the tissue by ultrasound. This is like measuring the sound of thunder after lightning. Measurements together with mathematics provide ideas about the inside. The technique combines the best of light and sound since good contrast from optical part - though with low resolution - while ultrasound has good resolution but poor contrast (since not enough absorption is going on). In PAT, the measurements are recorded at the surface of the tissue by an array of ultrasound sensors. Each of that only detects the field over a small volume of space, and the measurement continues only for a finite time. In order to form a PAT image, it is necessary to solve an inverse initial value problem by inferring an initial acoustic pressure distribution from measured acoustic time series. In many practical imaging scenarios it is not possible to obtain the full data, or the data may be sub-sampled for faster data acquisition. Then numerical models of wave propagation can be used within the variational image reconstruction framework to find a regularized least-squares solution of an optimization problem. Assuming homogeneous acoustic properties and the absence of acoustic absorption the measured time series can be related to the initial pressure distribution via the spherical mean Radon transform. Integral geometry can be used to derive direct, explicit inversion formulae for certain sensor geometries, such as e.g. spherical arrays. At the moment PAT is predominantly used in preclinical setting, to image tomours and vasculature in small animals. Breast imaging, endoscopic fetus imaging as well as monitoring of perfusion and drug metabolism are subject of intensive ongoing research. The forward problem is related to the absorption of the light and modeled by the wave equation assuming instanteneous absorption and the resulting thearmal expansion. In our case, an optical ultrasound sensor records acoustic waves over time, i.e. providing time series with desired spacial and temporal resolution. Given complete data, then one can mathematically reverse the time direction and find out the original object. Often it is not possible to collect a complete data due to e.g. single sided access to the object as in breast imaging or underlying dynamics happening on a faster rate than one can collect data. In such situations one can formulate the problem in variational framework using regularisation to compensate for the missing data. In particular in subsampling scenario, one would like to use raytracing methods as they scale linearly with the number of sensors. Marta's group is developing flexible acoustic solvers based on ray tracing discretisation of the Green's formulas. They cannot handle reflections but it is approximately correct to assume this to be true as the soundspeed variation is soft tissue is subtle. These solvers can be deployed alongside with stochastic iterative solvers for efficient solution of the variational formulation. Marta went to school in Poland. She finished her education there in a very selected school and loved math due to a great math teacher (which was also her aunt). She decidede to study Computer Sciences, since there she saw more chances on the job market. When moving to Germany her degree was not accepted, so she had to enrol again. This time for Computer Sciences and Engineering at the Hamburg University of Technology https://www.tuhh.de/alt/tuhh/startpage.html. After that she worked on her PhD in the small group of Heinrich Voss https://www.mat.tuhh.de/home/hvoss_en there. She had good computing skills and fit in very well. When she finished there she was married and had to solve a two body problem, which brought the couple to Manchester, where a double position was offered. Now both have a permanent position in London. REFERENCES __ __ PODCASTS __ __ __ __

45m

Feb 27, 2020

This is the third of three conversation recorded during the Conference on mathematics of wave phenomena https://conference18.waves.kit.edu/ 23-27 July 2018 in Karlsruhe. Gudrun is in conversation with Anne-Sophie Bonnet-BenDhia https://uma.ensta-paristech.fr/~bonnet from ENSTA https://uma.ensta-paristech.fr/ in Paris about transmission properties in perturbed waveguides. The spectral theory https://en.wikipedia.org/wiki/Spectral_theory is essential to study wave phenomena. For instance, everybody has experimented with resonating frequencies in a bathtube filled with water. These resonant eigenfrequencies https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors#Vibration_analysis are eigenvalues of some operator which models the flow behaviour of the water. Eigenvalue problems are better known for matrices. For wave problems, we have to study eigenvalue problems in infinite dimension. Like the eigenvalues for a finite dimensional matrix the Spectral theory gives access to intrinisic properties of the operator and the corresponding wave phenomena. Anne-Sophie is interested in waveguides. For example, optical fibres https://en.wikipedia.org/wiki/Optical_fiber can guide optical waves while wind instruments https://en.wikipedia.org/wiki/Wind_instrument are guides for acoustic waves. Electromagnetic waveguides also have important applications. A practical objective is to optimize the transmission in a waveguide, even if there are some perturbations inside. It is known that for certain frequencies, there is no reflection by the perturbations but it is not apriori clear how to find these frequencies. Anne-Sophie uses complex analysis https://en.wikipedia.org/wiki/Complex_analysis for that. The idea is to complexify the (originally real) coordinates by analytic extension https://en.wikipedia.org/wiki/Analytic_continuation. It is a classic idea for resonances that she adapts to the problem of transmission. This mathematical method of complex scaling is linked to the method of perfectly matched layers in numerics. It is used to solve problems set in unbounded domains on a computer by finite elements. Thanks to the complex scaling, she can solve a problem in a bounded domain, which reproduces the same behaviour as in the infinite domain. Finally, Anne-Sophie is able to get numerically a complex spectrum of frequencies, related to the quality of the transmission in a perturbed waveguide. The imaginary part of the complex quantity gives an indication of the quality of the transmission in the waveguide. The closer to the real axis the better the transmission. REFERENCES __ __ PODCASTS __ __

31m

Feb 06, 2020

* Gudrun sprach im Januar 2020 mit drei Studenten ihrer Vorlesung Mathematical Modelling and Simulation: Samory Gassama, Lennart Harms und David Schneiderhan. Sie hatten in ihrem Projekt Gruppenentscheidungen modelliert. In dem Gespräch geht es darum, wie man hierfür mathematische Modelle findet, ob man Wahlsysteme fair gestalten kann und was sie aus den von ihnen gewählten Beispielen gelernt haben. Wie lassen sich Entscheidungen von Wählergruppen fair in demokratische Willensbildung einbringen? Mit diesem Thema beschäftigt sich u.a. auch die Volkswirtschaftslehre. Die dafür benutzten Modelle sollten einige Eigenschaften haben. Ein grundlegendes Kriterium wäre beispielsweise: Wenn alle der gleichen Meinung sind, sollte diese Meinung auch immer die Gruppenentscheidung sein. Ein weiteres Kriterum könnte verlangen, dass das Ergebnis Pareto-optimal https://de.wikipedia.org/wiki/Pareto-Optimum ist, es also kein anderes Ergebnis gibt, mit dem jedes Gruppenmitglied zufriedener wäre. Um die Präferenz der Gruppe auszudrücken, führen die Studenten die Wohlfahrtsfunktion ein. Das ist eine Abbildung, welche als Input die Präferenzen der einzelnen Wähler verknüpft. Das Wahlverfahren wird sozusagen in dieser Abbildung modelliert. Man wünscht sich __ __ Verfahren wie Rangaddition https://de.wikipedia.org/wiki/Borda-Wahl und Condorcet-Methode https://de.wikipedia.org/wiki/Condorcet-Methode sind klassisch und erfüllen leider nicht alle diese Bedingungen. Die Studenten fügen eine weitere Entscheidungsebene im Modell hinzu. Man nennt dies geschachtelte Wahl. Als Beispiele dienen die US Präsidentschaftswahl 2016 und der Eurovision Song Contest https://de.wikipedia.org/wiki/Eurovision_Song_Contest 2019. Bei den Präsidentschaftswahlen in den VereinigtenStaaten von Amerika https://de.wikipedia.org/wiki/Electoral_College, wird der Präsident von den Wahlleuten https://de.wikipedia.org/wiki/Wahlmann der Bundesstaaten für eine Amtszeit bestimmt. Jeder Bundesstaat hat unterschiedlich viele Wahlleute. Die Wahlberechtigten legen unmittelbar nur die Wahlleute fest. Deshalb ist das Modell der US Präsidentschaftswahlen ist ein geschachteltes Modell. Im ersten Schritt, werden in allen 52 Staaten die Wahlen, mit den US Bürgern des jeweiligen Staates als Wähler, mithilfe des Condorcet Modells durchgeführt. Im zweiten Schritt bilden eben jene 52 Staaten die neue Wählermenge, welche dann über eine gewichtete Rangaddition den endgültigen Präsidenten bestimmt. Die Studenten haben im Projekt zwei Datensätze verwendet, um die Präsidentschaftswahlen 2016 in den USA zwischen Donald Trump und Hillary Clinton zu simulieren. Sie geben die Anzahl der Stimmen für Donald Trump und Hillary Clinton in den verschiedenen Wahlbezirken der USA an. Um die Simulation durchzuführen, wurde Google Colab verwendet. Die benutzte Programmiersprache ist Python. Die Wahl wurde folgendermaßen simuliert: Man summiert die Anzahl der Stimmen für alle Kandidaten in jedem Staat. Anschließend vergleicht man die Anzahl der Stimmen für Trump und Clinton in jedem Bundesstaat. Dem Gewinner eines Staates werden die Anzahl der Wahlleute dieses Bundesstaates in das Endergebnis addiert. Zum Schluss werden die Anzahl der Wahlleute, welche für die Kandidaten gestimmt haben verglichen. Trump gewinnt die Wahlen in 30 Bundesstaaten und Clinton in 20 Bundesstaaten, genauer gesagt erhält Trump 304 Wahlleute und Clinton 227. Somit wäre gewinnt Trump gegen Clinton. Alternativ zum geschachtelten Modell, wird anschließend die Abstimmungsmethode direkt auf alle Wahlstimmen angewandt. Dabei erhält Trump 62.984.828 Stimmen, während Clinton 65.853.514 bekommt. Bei diesem Verfahren gewinnt Clinton gegen Trump. Im Gespräch wird besprochen, dass es ein Problem ist, wenn bei recht knappem Wahlausgang pro Bundesstaat eine "Rundung" auf Wahlleute erfolgt und diese dann addiert wird. Im Vergleich hierzu kann es bei vielen Parteien auch durch Instrumente wie die 5%-Hürde, die wir in Deutschland implementiert haben, zu unfairen Effekten kommen. Die Regeln beim Eurovision Song Contest https://de.wikipedia.org/wiki/Eurovision_Song_Contest sind wie folgt: Aus den Televoting-Ergebnissen und den Jurywertungen jedes einzelnen Landes setzt sich das Gesamtergebnis für alle Teilnehmenden zusammen. Die besten zehn Titel werden mit eins, zwei, drei, vier, fünf, sechs, sieben, acht, zehn und zwölf Punkten bewertet. Dabei werden die Jury- und Zuschauerwertungen seit 2016 voneinander getrennt. Jedes Land kann einem Teilnehmenden also bis zu 24 Punkte geben - zwölf durch die Jury, zwölf durch die Zuschauer. Wenn zwei Songs auf die gleiche Punktzahl kommen, bekommt das Land die höhere Punktzahl, das vom Publikum höher bewertet wurde. Abgesehen davon, dass es sich auch hierbei wieder um ein geschachteltes Modell handelt, werden hierbei auch noch die gewichtete Rangaddition und ein externes Diktator Modell verwendet. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

34m

Jan 31, 2020

* Gudruns Arbeitsgruppe begrüßte im Januar 2020 Andrea Walther https://www.mathematik.hu-berlin.de/de/forschung/forschungsgebiete/mathematische-optimierung/andrea-walther/ als Gast. Sie ist Expertin für das algorithmische Differenzieren https://de.wikipedia.org/wiki/Automatisches_Differenzieren (AD) und ihre Arbeitsgruppe ist verantwortlich für das ADOL-C https://projects.coin-or.org/ADOL-C Programmpaket zum algorithmischen Differenzieren. Zusammen mit Andreas Griewank hat sie 2008 das Standardbuch zu AD https://my.siam.org/Store/Product/viewproduct/?ProductId=1005 veröffentlicht. Im Abitur und im mathematischen Grundstudium lernt jede und jeder Anwendungen kennen, wo Ableitungen https://de.wikipedia.org/wiki/Differentialrechnung#Ableitungsfunktion von Funktionen gebraucht werden. Insbesondere beim Auffinden von Minima und Maxima https://de.wikipedia.org/wiki/Extremwert von Funktionen ist es sehr praktisch, dies als Nullstellen der Ableitung zu finden. Bei der Modellierung komplexer Zusammenhänge mit Hilfe von partiellen Differentialgleichungen ist es möglich, diese Idee in ein abstrakteres Setting zu Übertragen. Eine sogenannte Kostenfunktion misst, wie gut Lösungen von partiellen Differentialgleichungen einer vorgegebenen Bedingung genügen. Man kann sich beispielsweise einen Backofen vorstellen, der aufgeheizt wird, indem am oberen und unteren Rand eine Heizspirale Wärme in den Ofen überträgt. Für den Braten wünscht man sich eine bestimmte Endtemperaturverteilung. Die Wärmeverteilung lässt sich mit Hilfe der Wärmeleitungsgleichung berechnen. In der Kostenfunktion wird dann neben der gewünschten Temperatur auch noch Energieeffizienz gemessen und die Abweichung von der Endtemperatur wird zusammen mit der benötigten Energie minimiert. Auch hierzu werden Ableitungen berechnet, deren Nullstellen helfen, diese Kosten zu minimeren. Man spricht hier von optimaler Steuerung. Eine Möglichkeit, die abstrakte Ableitung auszudrücken, ist das Lösen eines sogenannten adjungierten partiellen Differenzialgleichungsproblems. Aber hier wird es sehr schwierig, immer schnell und fehlerfrei Ableitungen von sehr komplexen und verschachtelten Funktionen zu berechnen, zumal sie für jedes Problem immer wieder neu und anders aussehen. Außerdem braucht man in der numerischen Auswertung des Algorithmus oft nur Werte dieser Ableitung an bestimmten Stellen. Deshalb ist die effiziente Berechnung von Funktionswerten der Ableitung ein unverzichtbarer Baustein in zahlreichen Anwendungen, die von Methoden zur Lösung nichtlinearer Gleichungen bis hin zu ausgefeilten Simulationen in der Optimierung und optimalen Kontrolle reichen. Am liebsten sollte dies der Computer fehlerfrei oder doch mit sehr kleinen Fehlern übernehmen können. Auch für das Newtonverfahren https://de.wikipedia.org/wiki/Newtonverfahren braucht man die Ableitung der Funktion. Es ist das Standardverfahren zur Lösung nichtlinearer Gleichungen und Gleichungssysteme. Das algorithmische Differenzieren (AD) liefert genaue Werte für jede Funktion, die in einer höheren Programmiersprache gegeben ist, und zwar mit einer zeitlichen und räumlichen Komplexität, die durch die Komplexität der Auswertung der Funktion beschränkt ist. Der Kerngedanke der AD ist die systematische Anwendung der Kettenregel der Analysis. Zu diesem Zweck wird die Berechnung der Funktion in eine (typischerweise lange) Folge einfacher Auswertungen zerlegt, z.B. Additionen, Multiplikationen und Aufrufe von elementaren Funktionen wie zum Beispiel Exponentialfunktion oder Potenzen. Die Ableitungen bezüglich der Argumente dieser einfachen Operationen können leicht berechnet werden. Eine systematische Anwendung der Kettenregel ergibt dann die Ableitungen der gesamten Sequenz in Bezug auf die Eingangsvariablen Man unterscheidet zwei Verfahren: den Vorwärts- und den Rückwärtsmodus. Im Vorwärtsmodus berechnet man das Matrizenprodukt der Jacobi-Matrix https://de.wikipedia.org/wiki/Jacobi-Matrix mit einer beliebigen Matrix (sogenannte Seedmatrix), ohne vorher die Komponenten der Jacobi-Matrix zu bestimmen. Der Rückwärtsmodus besteht aus zwei Phasen. Die Originalfunktion wird zunächst ausgeführt und gewisse Daten abgespeichert. Anschließend rechnet man rückwärts. Dabei werden Richtungsableitungen übergeben und es werden die im ersten Schritt gespeicherten Daten verwendet. Mit dem Rückwärtsmodus von AD ist es möglich, den Gradienten einer skalarwertigen Funktion mit Laufzeitkosten von weniger als vier Funktionsauswertungen zu berechnen. Diese Grenze ist auch noch völlig unabhängig von der Anzahl der Eingangsvariablen. Das ist phänomenal effektiv, aber er ist mit einem erhöhten Speicherbedarf verbunden. Im Laufe der Jahre wurden Checkpointing-Strategien entwickelt, um einen goldenen Mittelweg zu finden. Die Methoden sind für viele und sehr unterschiedliche Anwendungen interessant. In DFG-Projekten an denen Andrea beteiligt war und ist, wurde das unter anderem für die Modellierung von Piezokeramiken und für die Maxwellsche Wellengleichung umgesetzt. Außerdem sprechen Gudrun und Andrea über die Optimierung der Form einer Turbinenschaufel. Andrea begann ihre berufliche Laufbahn mit einer Ausbildung zur Bankkauffrau in Bremerhaven. Sie entschied sich anschließend für ein Studium der Wirtschaftsmathematik, um Mathematik und ihren erlernten Beruf zusammen zu halten. Unter den wenigen verfügbaren Standorten für so ein Studium in Deutschland entschied sie sich für die Universität Bayreuth. Nach Abschluss des Diploms gab es die Chance, an der TU Dresden im Optimierungsfeld zu arbeiten. Dort promovierte sie, wurde es später Leiterin der selbständigen Nachwuchsgruppe "Analyse und Optimierung von Computermodellen", Juniorprofessorin für "Analyse und Optimierung von Computermodellen" und habilitierte sich. 2009-2019 war sie als Professorin für "Mathematik und ihre Anwendungen" an der Universität Paderborn tätig. Seit Oktober 2019 ist sie Professorin für "Mathematische Optimierung", Humboldt-Universität zu Berlin. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

1h 8m

Jan 23, 2020

* This is the second of three conversation recorded Conference on mathematics of wave phenomena https://conference18.waves.kit.edu/ 23-27 July 2018 in Karlsruhe. Gudrun is in conversation with Mariana Haragus http://members.femto-st.fr/mariana-haragus/en about Benard-Rayleigh problems https://en.wikipedia.org/wiki/Rayleigh%E2%80%93B%C3%A9nard_convection. On the one hand this is a much studied model problem in Partial Differential Equations. There it has connections to different fields of research due to the different ways to derive and read the stability properties and to work with nonlinearity. On the other hand it is a model for various applications where we observe an interplay between boyancy and gravity and for pattern formation in general. An everyday application is the following: If one puts a pan with a layer of oil on the hot oven (in order to heat it up) one observes different flow patterns over time. In the beginning it is easy to see that the oil is at rest and not moving at all. But if one waits long enough the still layer breaks up into small cells which makes it more difficult to see the bottom clearly. This is due to the fact that the oil starts to move in circular patterns in these cells. For the problem this means that the system has more than one solutions and depending on physical parameters one solution is stable (and observed in real life) while the others are unstable. In our example the temperature difference between bottom and top of the oil gets bigger as the pan is heating up. For a while the viscosity and the weight of the oil keep it still. But if the temperature difference is too big it is easier to redistribute the different temperature levels with the help of convection of the oil. The question for engineers as well as mathematicians is to find the point where these convection cells evolve in theory in order to keep processes on either side of this switch. In theory (not for real oil because it would start to burn) for even bigger temperature differences the original cells would break up into even smaller cells to make the exchange of energy faster. In 1903 Benard did experiments similar to the one described in the conversation which fascinated a lot of his colleagues at the time. The equations where derived a bit later and already in 1916 Lord Rayleigh found the 'switch', which nowadays is called the critical Rayleigh number. Its size depends on the thickness of the configuration, the viscositiy of the fluid, the gravity force and the temperature difference. Only in the 1980th it became clear that Benards' experiments and Rayleigh's analysis did not really cover the same problem since in the experiment the upper boundary is a free boundary to the surrounding air while Rayleigh considered fixed boundaries. And this changes the size of the critical Rayleigh number. For each person doing experiments it is also an observation that the shape of the container with small perturbations in the ideal shape changes the convection patterns. Maria does study the dynamics of nonlinear waves and patterns. This means she is interested in understanding processes which change over time. Her main questions are: __ __ She treats her problems with the theory of dynamical systems and bifurcations. The simplest tools go back to Poincaré when understanding ordinary differential equations. One could consider the partial differential equations to be the evolution in an infinite dimensional phase space. Here, in the 1980s, Klaus Kirchgässner had a few crucial ideas how to construct special solutions to nonlinear partial differential equations. It is possible to investigate waterwave problems which are dispersive equations as well as flow problems which are dissipative. Together with her colleagues in Besancon she is also very keen to match experiments for optical waves with her mathematical analysis. There Mariana is working with a variant of the Nonlinear Schrödinger equation called Lugiato-Lefever Equation. It has many different solutions, e.g. periodic solutions and solitons. Since 2002 Mariana has been Professor in Besancon (University of Franche-Comté, France). Before that she studied and worked in a lot of different places, namely in Bordeaux, Stuttgart, Bucharest, Nice, and Timisoara. REFERENCES __ __ PODCASTS __ __

30m

Jan 16, 2020

* * This is the first of three conversation recorded Conference on mathematics of wave phenomena https://conference18.waves.kit.edu/ 23-27 July 2018 in Karlsruhe. Gudrun talked to Fioralba Cakoni http://sites.math.rutgers.edu/~fc292/ about the Linear Sampling Method and Scattering https://en.wikipedia.org/wiki/Scattering. The linear sampling method https://iopscience.iop.org/article/10.1088/0266-5611/20/1/010/meta is a method to reconstruct the shape of an obstacle without a priori knowledge of either the physical properties or the number of disconnected components of the scatterer. The principal problem is to detect objects inside an object without seeing it with our eyes. So we send waves of a certain frequency range into an object and then measure the response on the surface of the body. The waves can be absorbed, reflected and scattered inside the body. From this answer we would like to detect if there is something like a tumor inside the body and if yes where. Or to be more precise what is the shape of the tumor. Since the problem is non-linear and ill posed this is a difficult question and needs severyl mathematical steps on the analytical as well as the numerical side. In 1996 Colton and Kirsch (reference below) proposed a new method for the obstacle reconstruction problem in inverse scattering which is today known as the linear sampling method. It is a method to solve the above stated problem, which scientists call an inverse scattering problem. The method of linear sampling combines the answers to lots of frequencies but stays linear. So the problem in itself is not approximated but the interpretation of the response is. The central idea is to invert a bounded operator which is constructed with the help of the integral over the boundary of the body. Fioralba got her Diploma (honor’s program) and her Master's in Mathematics at the University of Tirana. For her Ph.D. she worked with George Dassios from the University of Patras https://en.wikipedia.org/wiki/University_of_Patras but stayed at the University of Tirana. After that she worked with Wolfgang Wendland at the University of Stuttgart as Alexander von Humboldt Research Fellow https://en.wikipedia.org/wiki/Alexander_von_Humboldt_Foundation. During her second year in Stuttgart she got a position at the University of Delaware https://en.wikipedia.org/wiki/University_of_Delaware in Newark https://en.wikipedia.org/wiki/Newark,_Delaware. Since 2015 she has been Professor at Rutgers University https://en.wikipedia.org/wiki/Rutgers_University. She works at the Campus in Piscataway https://en.wikipedia.org/wiki/Piscataway,_New_Jersey near New Brunswick https://en.wikipedia.org/wiki/New_Brunswick,_New_Jersey (New Jersey). REFERENCES __ __ PODCASTS __ __

47m

Jan 09, 2020

Emmy Noether https://de.wikipedia.org/wiki/Emmy_Noether, eine der bedeutendsten Mathematiker*innen weltweit, prägte mit ihren „Arbeits- und Auffassungsmethoden“ die moderne Algebra und trug entscheidend zur Algebraisierung mathematischer Disziplinen bei. Mit ihrer 1918 publizierten Habilitationsschrift löste sie zentrale mathematische Probleme der allgemeinen Relativitätstheorie. Am 4. Juni 1919 hielt Emmy Noether ihren Habilitationsvortrag. Sie war die erste Frau, die in Preußen habilitiert wurde. Genau 100 Jahre später stellte in Berlin eine interdisziplinäre Fachkonferenz deshalb die Frage: „Wie kommt das Neue in die Welt?“ Die Tagung wurde gemeinsam veranstaltet vom Berliner Exzellenzcluster MATH+ http://www.mathplus.de/, der Zentralen Frauenbeauftragten der Freien Universität Berlin und dem Max-Planck-Institut für Wissenschaftsgeschichte https://www.mpiwg-berlin.mpg.de/de. Aus mathematischer, physikalischer, wissenschaftstheoretischer und ‑historischer Perspektive beleuchtete die Konferenz die Bedeutung Noethers bis in die Gegenwart. Darüber hinaus nahm sie Strukturen und Prozesse der Diskriminierung und Marginalisierung in den Blick, die Noether als Frau jüdischer Herkunft im deutschen Wissenschaftssystem widerfuhren und die Rezeption ihrer mathematischen Leistungen auch über ihren Tod hinaus beeinträchtigten. Den Abschluss bildete am 6. Juni 2019 eine öffentliche Podiumsdiskussion zur Frage "Wie kommt das Neue in die Welt? Reflexionen über das Verhältnis von Mathematik, Gesellschaft, Geschlecht und Diversität" unter Moderation von Jan-Martin Wiarda https://www.jmwiarda.de/ (Wissenschaftsjournalist). Das Gespräch hat Gudrun für unseren Podcast mitgeschnitten. Auf dem Podium waren vertreten: __ __ Außerdem spricht am Ende des Mitschnittes __ __ Im Gespräch wird erörtert, inwieweit es zu Konflikten mit der Fachdisziplin Mathematik führt, wenn der Blick auch auf geschlechtergerechte Ausbildung - insbesondere im Lehramt - gelenkt wird. Anina Mischau hat hier Pionierarbeit in der Mathematik an der FU Berlin geleistet. Dort hat sie inzwischen den Eindruck, dass die Arbeit geschätzt wird. Bei der Untersuchung des Anteils von Frauen in den hoch renommierten Fachzeitschriften und auf den alle vier Jahre stattfindenden Intermationalen Konferenzen für Mathematik sind die Zahlen allerdings noch nicht sehr ermutigend. Selbst die relativ gibt es kaum Verbesserungen. Es stellt sich automatisch die Frage, wo diese Unterschiede herkommen. Im Gespräch wird erläutert, inwieweit der fachinterne Wettbewerb männlich geprägt ist und durch welche Maßnahmen es hier eine Veränderung geben kann. Für jede einzelne Berufung ist es nicht so offensichtlich, wie man hier Gerechtigkeit schaffen kann, wenn die Bewerberlage schon eine Schieflage hat. Die massive Nutzung von zählbaren Größen als wichtiges Kriterium im Vergleich ist ja eigentlich erst sehr jungen Datums und ist für die Arbeit als Professor bzw. Professorin nur ein Anhaltspunkt unter vielen für die Eignung. Die DFG hat hier schon einige ganz gute Ideen implementiert. z.B. in der Vorgabe nur eine vorgegebene Anzahl von Veröffentlichungen beizufügen, die relevant sind und auch von Gutachtern in ihr Bild einbezogen werden können (statt Anzahlen zu vergleichen). Frauen müssen schon früh von außen Bestätigung bekommen, wenn sie sich als begabt und geeignet zeigen. Das Übersehen von Talent abseits der ausgetretenen Pfade wird sich in jedem Fall als Nachteil für jede Bildungseinrichtung auswirken. Häufig geht es hier auch um Themenfelder, die etwa abseits der Trends liegen. Das Theaterstück „Mathematische Spaziergänge mit Emmy Noether" kann am 10. Dezember 2019 in Göttingen sowie am 12. Mai 2020 in München besucht werden. Das Exzellenzclusters MATH+ https://mathplus.de/ ist ein institutionenübergreifender und transdisziplinärer Exzellenzcluster. Ziel ist es, neue Ansätze in der anwendungsorientierten Mathematik zu erforschen und weiterzuentwickeln. Der Schwerpunkt liegt auf mathematischen Prinzipien zur Nutzung immer größerer Datenmengen in den Lebens- und Materialwissenschaften, in der Energie- und Netzwerkforschung sowie in den Geistes- und Sozialwissenschaften. Innerhalt des Clusters gibt es auch ein soziologisches Projekt, das die Karrierewege der beteiligten jungen Wissenschaftler und Wissenschaftlerinnen über einen längeren Zeitraum begleiten und untersuchen wird. MATH+ wird von der DFG für einen ersten Zeitraum von sieben Jahren seit Januar 2019 gefördert. Es ist ein Gemeinschaftsprojekt der drei großen Berliner Universitäten - Freie Universität Berlin, Humboldt-Universität zu Berlin und Technische Universität Berlin - sowie des Weierstraß-Instituts für Angewandte Analysis und Stochastik (WIAS) und des Zuse Instituts Berlin (ZIB). MATH+ setzt die Erfolgsgeschichten des renommierten Forschungszentrums MATHEON und der Excellence-Graduate School Berlin Mathematical School (BMS) fort. DIE REFERENT*INNEN IM DETAIL Prof. Dr. Katja Eilerts https://www.noetherkonferenz2019.de/listenordner-referent_innen/Eilerts/index.html Professorin für Grundschulpädagogik, Dr. rer. nat., promovierte in der Fakultät für Informatik, Elektrotechnik und Mathematik an der Universität Paderborn; 1997-2000 Studium des Lehramtes für die Primarstufe, Universität Paderborn; seit 2014 W2-Professorin für Grundschulpädagogik - Lernbereich Mathematik an der Humboldt Universität zu Berlin; 2012 Ruf auf eine W2-Professur an der Freien Universität Berlin (abgelehnt); 2012-2014 W2-Professorin für Grundschulpädagogik/Mathematik an der Universität Potsdam; 2011-2012 Gast-Professorin an der Freien Universität Berlin; 2009-2011 Vertretungs-Professorin an der Universität Kassel im Bereich der Mathematik-Didaktik; 2007-2009 Wissenschaftliche Mitarbeiterin, Fakultät für Informatik, Elektrotechnik und Mathematik, Universität Paderborn; 2005-2007 Stipendiatin des Graduiertenkollegs der Universität Paderborn & Lehrauftrag an der Fakultät für Informatik, Elektrotechnik und Mathematik, Universität Paderborn. Prof. Dr. Rupert Klein https://www.noetherkonferenz2019.de/listenordner-referent_innen/Klein/index.html Professor für numerische Strömungsmechanik an der Freien Universität Berlin. 1979-1983 Studium Maschinenbau an der RWTH Aachen; Promotion 1988 in Maschinenbau; 1988-1990 Post-Doktorand, Mathematik, Princeton University; ab 1991 wissenschaftlicher Assistent in Aachen; 1995 Habilitation; 1996/97 Professor für Sicherheitstechnik an der Bergischen Universität Wuppertal; 1997-2007 Abteilungsleiter Data & Computation am Potsdam-Institut für Klimafolgenforschung (2006-2007 stellv. Direktor); ab 1997 Professor für Wissenschaftliches Rechnen (Scientific Computing) und Modellierung und Simulation globaler Umweltsysteme an der FU Berlin. Dr. Mechthild Koreuber https://www.noetherkonferenz2019.de/listenordner-referent_innen/Koreuber/index.html Dipl. Mathematikerin, promovierte Mathematikhistorikerin; Studium der Mathematik, Geschichte, Politikwissenschaften und Philosophie an der Freien Universität Berlin; 1990–1998 wissenschaftliche Mitarbeiterin in der theoretischen Informatik an der Technischen Universität Berlin; seit 1999 hauptberufliche Zentrale Frauenbeauftragte der Freien Universität Berlin; 2015 Promotion über Emmy Noether und die Noether-Schule. Prof. Dr. Helena Mihaljević https://www.noetherkonferenz2019.de/listenordner-referent_innen/Mihaljevic/index.html Promovierte Mathematikerin, Studium der Mathematik an der Georg-August-Universität Göttingen; 2006–2009 Promotion in Mathematik an der University of Liverpool zu Topologischer Dynamik ganzer transzendenter Funktionen; 2009–2011 wissenschaftliche Mitarbeiterin am Mathematischen Seminar der Christian-Albrechts-Universität zu Kiel; 2011–2014 Editorin und stellvertretende Abteilungsleiterin bei FIZ Karlsruhe – Leibniz Institut für Informationsinfrastruktur, Abteilung Mathematik und Informatik; 2014–2018 Senior Data Scientist bei The unbelievable Machine Company, Berlin; seit 2018 Professorin für Data Science an der Hochschule für Technik und Wirtschaft (HTW) Berlin (Professur gehört zum Einstein Center Digital Future https://www.digital-future.berlin/). Dr. Anina Mischau https://www.noetherkonferenz2019.de/listenordner-referent_innen/Mischau/index.html Soziologin 2002-2013 wissenschaftliche Mitarbeiterin am Interdisziplinären Zentrum für Frauen- und Geschlechterforschung (IFF) der Universität Bielefeld; 2012-2015 Gastprofessur für „Gender Studies in der Mathematik und Didaktik der Mathematik“ am FB Mathematik und Informatik der Freien Universität Berlin; 2015-2016 Gastprofessur zur „Integration von Genderkompetenz in die Lehramtsausbildung Primarstufe Mathematik“ am Institut für Erziehungswissenschaften, Abteilung Grundschulpädagogik – Lernbereich Mathematik der Humboldt-Universität zu Berlin; seit 2016 wissenschaftliche Mitarbeiterin am FB Mathematik und Informatik der FU Berlin, Leiterin der Arbeitsstelle „Gender Studies in der Mathematik“. Prof. Dr. Caren Tischendorf https://www.noetherkonferenz2019.de/listenordner-referent_innen/Tischendorf/index.html Studium der Mathematik in Berlin und Moskau; 1996 Promotion an der Humboldt-Universität zu Berlin in Numerischer Analysis, 2002-2004 Vorsitzende der Nachwuchsforschungsgruppe Numerische Analysis am DFG-Forschungszentrum MATHEON; 2004 Habilitation in Mathematik an der Humboldt-Universität zu Berlin; 2004-2006 Gastprofessorin an der TU; 2006-2012 Professorin für Mathematik/Numerische Analysis (W2) an der Universität zu Köln; seit Mai 2012 Professorin für Angewandte Mathematik am Institut für Mathematik an der Humboldt-Universität. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ __ __ PODCASTS __ __

1h 3m

Nov 30, 2019

Gudrun traf im November 2019 Jan Richter. Er ist einer der Gründer der Batemo GmbH https://www.batemo.de/ in Karlsruhe. Mit den Kollegiaten von SiMET http://www.simet.kit.edu/ hatte Gudrun das Unternehmen kurz vorher in der Technologiefabrik besucht und dabei das Podcast-Gespräch vereinbart. Batemo ist noch ein recht junges Unternehmen. Es wurde im März 2017 von Michael Schönleber und Jan Richter gegründet. Die beiden haben an der KIT-Fakultät für Elektrotechnik und Informationstechnik http://www.etit.kit.edu/index.php promoviert. Sie hatten sich schon länger mit der Idee auseinandergesetzt, im Anschluss an die Promotionszeit den Schritt zur Unternehmensgründung zu wagen. Es war klar, dass sie sich mit einem Thema beschäftigen möchten, das Ihnen ermöglicht, die Entwicklung von Akkus zu beeinflussen. Außerdem wollten sie gern ohne finanzielle Fremdmittel auskommen, um in jedem Moment die volle Kontrolle zu behalten. Inzwischen ist das gut gelungen und die Firma ist auf Simulationssoftware für Lithium-Ionen-Batterien https://de.wikipedia.org/wiki/Lithium-Ionen-Akkumulator spezialisiert. Für beliebige Lithium-Ionen-Zellen erstellen sie einen digitalen Zwilling, also ein Modell im Computer. Dass sie damit glaubwürdig für zahlungsfähige Kunden sind, liegt daran, dass sie auch die Validität dieser Modelle im gesamten Betriebsbereich nachweisen. Die Modelle sind sehr komplexe und stark nichtlinear gekoppelte Systeme aus algebraischen und partiellen Differentialgleichungen, die die physikalischen, chemischen und thermodynamische Prozesse abbilden. Sie sind auch dafür geeignet, das Verhalten der Akkus über die Lebenszeit der Zellen hin nachzubilden. Es ist besonders herausfordernd, da die Prozesse in unterschiedlichen Längen- und Zeitskalen ablaufen. Zwei Fragen, die beim Besuch mit den SiMET-Kollegiaten im Mittelpunkt des Gespräches standen, sind: __ __ Im Gespräch berichtet Jan auch davon, wieso er sich für ein Studium der Elektrotechnik entschieden hat und wie er den Weg in die Selbstständigkeit von heute aus bewertet. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

31m

Nov 23, 2019

Gudrun spricht mit Axel Voigt https://tu-dresden.de/mn/math/wir/das-institut/professuren. Er ist Professor für Wissenschaftliches Rechnen und Angewandte Mathematik an der TU Dresden https://tu-dresden.de/. Axel war Ende Oktober 2019 zu Gast in Gudruns Arbeitsgruppe, um seine Modelle für Kristallgitter zu diskutieren. Der Wunsch der Gruppe war, sowohl die Modelle als auch die dafür passenden numerischen Verfahren besser zu verstehen. Sie sind insbesondere für die Simulation der Vorgänge in Akkumulatoren interessant, die im Rahmen das Graduiertenkollegs SiMET http://www.simet.kit.edu/ vorangetrieben werden. Viele feste Körper haben eine Gitterstruktur. Für z.B. Silizium, Aluminium und Stahl ist dies ein Kristallgitter. In der Schule wird es der Einfachheit halber oft so dargestellt, als wäre das Kristallgitter eine feste Größe für solche Stoffe. In der Natur sind es aber polykristalline Materialien https://de.wikipedia.org/wiki/Polykristall. D.h. sie bestehen aus vielen unterschiedlichen Einzelkristallen. Diese sind durch Korngrenzen voneinander getrennt. Das Studium polykristalliner Materialien erfordert theoretische und rechnerische Techniken, die Untersuchungen auf unterschiedlich großen Skalen ermöglichen. Kristallgitterverformungen können mikroskopisch beschrieben werden, indem die Position der Atome explizit berücksichtigt wird, oder makroskopisch durch Kontinuumselastizität. Grobkörnige, mesoskalige Ansätze sind daher geeignete Werkzeuge, um Informationen über polykristalline Materialien bereitzustellen. In seiner Forschung betrachtet Axel sie als kontinuierliche elastische Felder, die aus einer atomistischen Darstellung der kristallinen Strukturen abgeleitet sind. So enthält sie auch wichtige Merkmale, die für die mikroskopische Skala typisch sind. Die Größe und Phase der Amplituden der Fourierspektrum https://de.wikipedia.org/wiki/Frequenzspektrum, zusammen mit der kontinuierlichen Beschreibung der Dehnungen, sind in der Lage, Kristalldrehungen, Gitterverformungen und Versetzungen zu charakterisieren. Darüber hinaus stellen sie in Kombination mit der so genannten Amplitudenerweiterung des Phasenfeld-Kristallmodells ein geeignetes Werkzeug zur Überbrückung mikroskopischer bis makroskopischer Skalen dar. Die Amplitudenerweiterung des Phasenfeld-Kristallmodells ermöglicht es, die Kristallgittereigenschaften auf diffusen Zeitskalen zu beschreiben, indem sie sich auf kontinuierliche Felder konzentriert, die auf Längenskalen variieren, die größer als der Atomabstand sind. So ermöglicht es die Simulation großer Systeme, die noch Details des Kristallgitters beibehalten. Axel Voigt hat an der TU München studiert und promoviert. Nach einem Ausflug in die Wirtschaft war er ab 2001 Gruppenleiter am Forschungsinstitut caesar in Bonn und hat sich dort auch habilitiert. Seit 2007 ist er in Dresden an der TU als Professor tätig. LITERATUR UND WEITERFÜHRENDE INFORMATIONEN __ __ PODCASTS __ __

33m

Nov 08, 2019

Gudrun talks to Anna Geyer https://annageyer.wordpress.com/. Anna is Assistant professer at TU Delft in the Mathematical Physics group https://www.tudelft.nl/en/eemcs/the-faculty/departments/applied-mathematics/mathematical-physics/ at the Delft Institute of Applied Mathematics https://www.tudelft.nl/en/ewi/the-faculty/departments/applied-mathematics/. She is interested in the behaviour of solutions to equations which model shallow water waves. The day before (04.07.2019) Anna gave a talk at the Kick-off meeting https://www.waves.kit.edu/kickoff2ndfundingperiod.php for the second funding period of the CRC Wave phenomena https://www.waves.kit.edu/ at the mathematics faculty in Karlsruhe, where she discussed instability of peaked periodic waves. Therefore, Gudrun asks her about the different models for waves, the meaning of stability and instability, and the mathematical tools used in her field. For shallow water flows the solitary waves are especially fascinating and interesting. Traveling waves are solutions of the form img representing waves of permanent shape f that propagate at constant speed c. These waves are called solitary waves if they are localized disturbances, that is, if the wave profile f decays at infinity. If the solitary waves retain their shape and speed after interacting with other waves of the same type, we say that the solitary waves are solitons. One can ask the question if a given model equation (sometimes depending on parameters in the equation or the size of the initial conditions) allows for solitary or periodic traveling waves, and secondly whether these waves are stable or unstable. Peaked periodic waves are an interesting phenomenon because at the wave crest (the peak) they are not smooth, a situation which might lead to wave breaking. For which equations are peaked waves solutions? And how stable are they? Anna answers these questions for the reduced Ostrovsky equation, which serves as model for weakly nonlinear surface and internal waves in a rotating ocean. The reduced Ostrovsky equation is a modification of the Korteweg-de Vries equation https://en.wikipedia.org/wiki/Korteweg%E2%80%93de_Vries_equation, for which the usual linear dispersive term with a third-order derivative is replaced by a linear nonlocal integral term, representing the effect of background rotation. Peaked periodic waves of this equation are known to exist since the late 1970's. Anna presented recent results in which she answers the long standing open question whether these solutions are stable. In particular, she proved linear instability of the peaked periodic waves using semi-group theory and energy estimates. Moreover, she showed that the peaked wave is unique and that the equation does not admit Hölder continuous solutions, which implies that the reduced Ostrovsky equation does not admit cusps. Finally, it turns out that the peaked wave is also spectrally unstable. This is joint work with Dmitry Pelinovsky https://dmpeli.math.mcmaster.ca/. For the stability analysis it is really delicate how to choose the right spaces such that their norms measure the behaviour of the solution. The Camassa-Holm equation https://en.wikipedia.org/wiki/Camassa%E2%80%93Holm_equation allows for solutions with peaks which are stable with respect to certain perturbations and unstable with respect to others, and can model breaking waves. Anna studied mathematics in Vienna. Adrian Constantin attracted her to the topic of partial differential equations applied to water waves. She worked with him during her PhD which she finished in 2013. Then she worked as Postdoc at the Universitat Autònoma de Barcelona https://www.uab.cat/en/ and in Vienna before she accepted a tenure track position in Delft in 2017. REFERENCES __ __ RELATED PODCASTS __ __

36m

Oct 31, 2019